Continuing my focus on Return to Ravnica Limited, in this article I look at a few of the interesting questions specific to the set. First, I calculate how risky it is to keep a starting hand that contains a Keyrune but not the land to cast it. Then I take a look at the most powerful Limited card in recent years: Pack Rat.

Keyrunes

The Keyrunes are great: mana fixing, acceleration, and a creature all on one card. Because they’re so great and because there are five of them, they see a lot of play. As such, I often find myself staring at the following starting hand: four spells, two lands, and a Keyrune. What should I do? Normally a three-mana hand is a keeper, but this one is a bit risky. How much worse is this hand than one with three lands? Should I keep? The same question applies to Axebane Guardian and Chromatic Lantern.

Drawing a third land is obviously the key. If I do, I have four mana. If I don’t, I stall at two, and that can lose me the game. What is the probability that I’ll draw a third land in time to cast my Keyrune on turn 3? I assume a 40-card deck with seventeen lands.

Those are high chances, but it’s not guaranteed. There’s reason to sweat, especially when I’m on the play.

Let’s say I don’t draw a land in time and don’t play my Keyrune on turn 3. How long, on average, will I have to wait? When can I expect to play the Keyrune if I miss turn 3?

Ouch. Turn 5 is pretty late; especially when you consider that the entire turn will be spent casting the Keyrune.

Perhaps I should mulligan. That raises the question of whether I can expect a six-card hand to be better. What is the probability that I’ll have three mana on turn 3 if I mulligan down to six cards and keep?

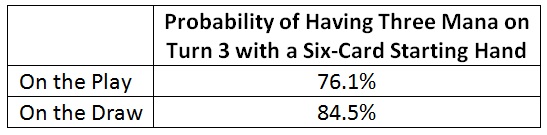
Interestingly, those probabilities aren’t much different. That probably means it’s better to keep the Keyrune hand. After all, if I get to three lands with the Keyrune, I have four mana. Also I’m up one card relative to the six-land hand. Still, I must consider the other cards in my hand. Is the hand mediocre for other reasons? Can the cards in this hand keep me alive if I stall at two mana?

It’s a tough decision, but knowing the above probabilities allows me to make the decision from an informed perspective.

Pack Rat

Pack Rat is an absurdly strong card. It takes over a game by itself and then wins that game. It’s so good I’ve heard stories of people playing decks with nothing put Pack Rats and Swamps. Of course, as soon as I heard that, I had to run the numbers. Sure, Pack Rat is awesome, but is it that good? Can I really win a tournament with the plan of mulling to Pack Rat? Let’s find out.

I’ll start modestly: a deck with one Pack Rat and 39 Swamps. I’ll mulligan until I either get the Pack Rat or I’m down to one card. What’s my chance of having Pack Rat on a given turn?

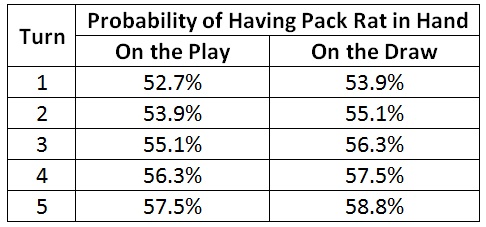
The probabilities are over 50%. Maybe this isn’t such a crazy idea. As I’d expect, the majority of my chance comes from finding the Rats during mulligans. The probability only goes up slightly during turns.

Winning

I’m merely trying to determine the feasibility of this strategy, so I don’t need to get an exact probability for winning. Estimating the odds is good enough. I’m going to say that if I have Pack Rat on turn 2, I win. If not, I lose. That’s obviously not completely accurate. Sometimes my early Pack Rat will get hit by an Electrickery. Sometimes I’ll draw it later and still win. But my approximation is close enough for the accuracy required.

Using that approximation and averaging on the play and on the draw, I have a 55% chance of winning game 1 with a single Pack Rat. What if I’ve got two or, god help my opponents, three Rats? My chance of winning goes up.

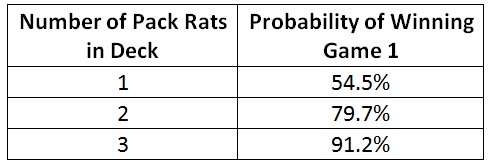
I have an 80% chance of winning with a two Rat deck. My lifetime win rate isn’t even close to that.

So what’s the probability I’ll win the full match? What’s the probability I’ll win two out of three games? I’ll assume losers always choose to play first.

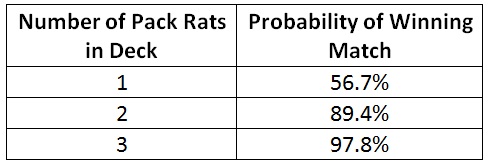
Ok, my real goal here is to blow out an FNM, right? What are my chances of a 5-0 record? That is equal to the probability of winning a match taken to the fifth power:

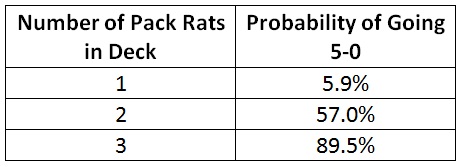
Clearly, I don’t want to try this when I’ve only got one Rat, but with two Rats I’ve got a 57% chance of going undefeated! That’s crazy! This isn’t just some urban legend. At two Rats, it’s a viable strategy. At three Rats, it’s probably the best deck you can make.

Obtaining Rats

Before I put the subject to bed, let’s check what the odds are of getting those Rats. I’ll consider the chance for both Sealed and at the Prerelease.

In Draft, I open three rares. I’ll assume no one ever passes Pack Rat, even on pack 3.

At the Prerelease, things were a bit more complicated. Azorius, Izzet, and Selesnya players opened five packs that could contain a Pack Rat. The guild pack for Golgari and Rakdos could also contain a Rat. Wizards has never been completely forthcoming about the contents of guild packs, so some speculation is required. I will assume that the distribution of cards across all guild packs is the same as the distribution across standard packs. Given that and since only two of the five guild packs can contain Pack Rat, the chance of Pack Rat being in a Golgari or Rakdos pack is 2.5 times higher than in a standard pack.

(Note that Wizards has stated that guild leaders are the only mythic rares that appear in guild packs. That indicates that the frequency of non-mythic rares might be slightly higher than I’m assuming.)

In the previous article, I determined that the probability of a pack containing a specific rare is 1.7%. Using my assumption about the contents of guild packs, that gives a 4.1% chance of pulling a Rat from a Golgari or Rakdos pack. That results in these probabilities of obtaining the necessary Pack Rats.

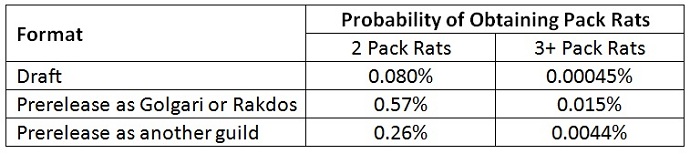
While the Prerelease numbers may be incorrect, as they depend on my assumption about the contents of guild packs, the numbers for draft are accurate.

Those percentages are small enough that I have a hard time wrapping my brain around them. Here’s an easier way to understand the probability. For each player that obtains enough Rats to make a Pack Rat deck, how many players do not?

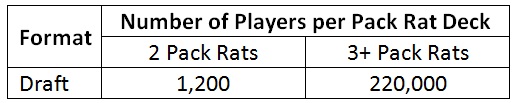
So one out of every 1200 players can play the two Rat deck at this Friday’s FNM. No surprise that the odds are very low, but they’re high enough that it will happen to a few people. Assuming about 30 people attend each FNM, one out of every 40 shops will have someone that can play the Pack Rat deck.

I’m hoping that person is me.

Takeaways

If you’re on the play and you keep a hand with two lands and a Keyrune, you have a 71% chance of casting the Keyrune on turn 3. On the draw, the chance is 85%.

If you pull two Pack Rats at FNM, consider playing a deck of only Rats and Swamps. You’ve probably got a better than even chance of going undefeated.

[email protected]
@DanRLN on Twitter
source code for the Magic Probability Toolkit