Limiting Chance is a series that uses statistics and probability to investigate topics relevant to Limited play. In this article, I look at a few questions specific to Return to Ravnica. First I calculate how hard gold cards are to cast relative to mono-colored cards. Then I investigate the deck thinning properties of Return to Ravnica’s land fetchers.
Casting Gold Cards
Gold cards are generally very strong for their converted mana costs. Even more so in Return to Ravnica, as Wizards wants the two-color theme at the forefront of play.
The justification given for the power of gold cards is usually:
- Gold cards can be played in fewer decks.
- Gold cards are harder to cast.
There’s no question that the first point is true. In pack one, picking a gold card is a greater commitment. In pack three, a gold card is less likely to be in my colors. If it’s not, I’ll need to devote picks to fixing or play with an awkward mana base.
But what about the second point? If I’m in the right colors, are gold cards harder to cast than mono-colored cards? Let’s investigate.
Bears
Is a spell that costs two different colors of mana significantly harder to cast than a spell that costs one mana of a single color?
To answer that question, let’s look Selesnya’s bears. (You probably already know this, but “bear” is slang for a two-mana 2/2.) Representing mono-colored cards is Keening Apparition, a perfectly serviceable two-drop that provides enchantment removal without thinning creature density. Representing gold is Vitu-Ghazi Guildmage, who has abilities that stay relevant long after its 2/2 body is outclassed. The Guildmage is clearly the stronger card because it’s a win condition in and of itself.
To characterize how hard each creature is to cast, I’ll use the chance of being able to cast that creature on turn 2. Of all possible turn 2 mana situations, in what percentage is the creature castable? I’m talking about Limited play, so I’ll use a 40-card deck with seventeen lands. Of those lands, I’ll say that eight are Plains, eight are Forests, and one is a Guildgate. I’ll do the calculation both on the draw and on the play, and I’ll average the results.
This calculation applies to spells of any color that have similar casting costs. So I’ll use the standard color-independent notation for casting costs where “C” represents the mana symbol of a card’s first color and “D” represents the mana symbol of that card’s second color.
Here are the probabilities of being able to cast each creature on turn 2.
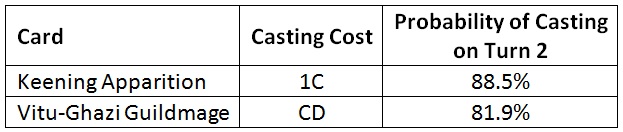
Vitu-Ghazi Guildmage is harder to cast than Keening Apparition, but not by much. In cases when I can cast the Apparition, I’ll be unable to cast the Guildmage less than 8% of the time. (That probability is obtained by dividing the chance of affording CD by the chance of affording 1C and then subtracting the result from one.)
Is 8% a small drop in casting chance? It would be good to have something to compare it to. For that, I look to mono-colored spells with two colored mana in their costs. I know that spells with that cost are harder to cast. How much harder? Knowing that will give me perspective on the probability I calculated for gold cards.
The Selesnya bear that fits the bill is Precinct Captain with its double-white cost. Here’s a table with the probability of casting each of the three creatures on turn 2. I’ve added an additional column that lists the probability of the creature being unaffordable in cases when I can afford Keening Apparition.

When I have the mana to cast the Apparition, the probability of not being able to cast the Guildmage is much lower than the probability of not being able to cast the Precinct Captain. Based on this comparison, it’s fair to characterize as small the less than 8% chance of not being able to cast the Guildmage.
I find that graphs are better than numbers at imparting an intuitive understanding of relative probability. So here’s a graph of the probability of affording various casting costs on turn 2.
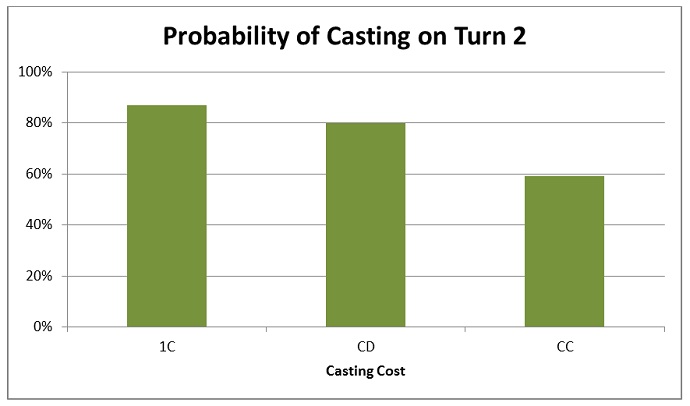
Gold cards are not significantly harder to cast than mono-colored spells with a single colored mana in their costs. That’s important to know when judging the power level of Return to Ravnica cards.
Drakes
Let’s expand this analysis to three-cost spells.
Azorius has a fleet of three-cost fliers in Return to Ravnica. Their costs range from extremely awkward (1CC for the Sunspire Griffin) to very convenient (1HH for the Vassal Soul, where “H” represents a hybrid mana). The relevant comparison for this analysis, however, is between Tower Drake at 2C and Lyev Skyknight at 1CD. The Skyknight is a more powerful card than the Drake. How much harder is it to cast?
Here are the probabilities of casting the creatures on turn 3. I’m using a deck similar to before with eight Plains, eight Islands, and one Azorius Guildgate.

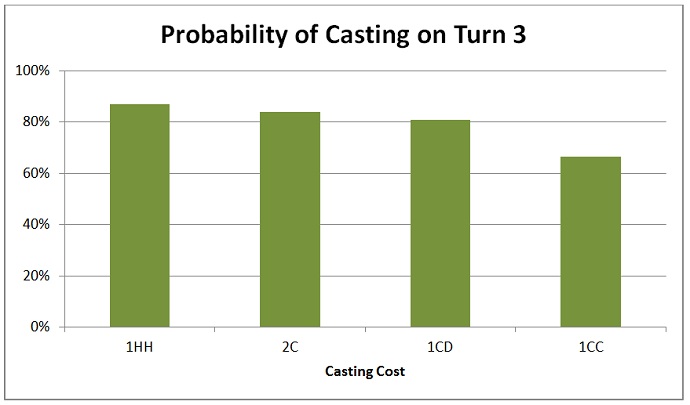
Again, the drop in probability from the mono-colored creature to the gold creature is very slight, even smaller than it was for two-mana spells. When I can cast Tower Drake, I’ll be unable to cast the Skyknight less than 4% of the time. That’s compared to the 21% of the time when I can’t cast the Griffin.
Here are the probabilities in a graph, including Vassal Soul’s cost as well.
A Simplified Example
So why is it that two mana of specified color is so much easier to come by when it’s of two different colors rather than two of a single color? Why is CD easier to pay than CC?
Some readers may already know the answer, but for those who don’t, let’s break things down with a simplified example. Say I have two basic lands. The first one is either a Forest or a Plains, and the second is also either a Forest or a Plains. Considering all possible combinations, how often can I pay GW and how often can I pay WW? Here’s a table of the combinations.
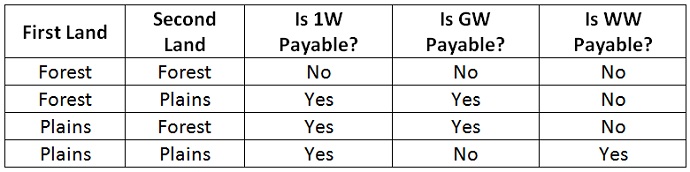
In two of the four cases I can cast the Guildmage. In only one of the four cases can I cast the Precinct Captain. There are more hands where the gold card is castable than the double white card. In a full game of Magic, things are obviously more complicated than that, but the same basic principle is at work. There are more starting hands that contain one of each basic land than starting hands that contain two of a specific land.
Uneven Land Splits
So far I’ve assumed that my deck splits its land evenly between colors. That is, of course, not always the case. I play with asymmetric mana bases all the time.
As the difference between the number of Forests and Plains in my deck increases, the chance of being able to cast gold cards decreases. Correspondingly, as the number of Plains increases, the chance of casting both Precinct Captain and Sunspire Griffon increases. That raises an interesting question. As the number of Plains increases, at what point does the casting chance of gold and double-white spells become equal?
Let’s first look at two-cost spells. To simplify the analysis, I won’t include a Guildgate in the deck. The deck will contain seventeen basic lands. Of those, the number of lands that produce C mana is listed in the table. The remaining lands produce D mana.
Here are the probabilities of being able to pay the given casting costs on turn 2 with various land splits, as calculated by the Magic Probability Toolkit.
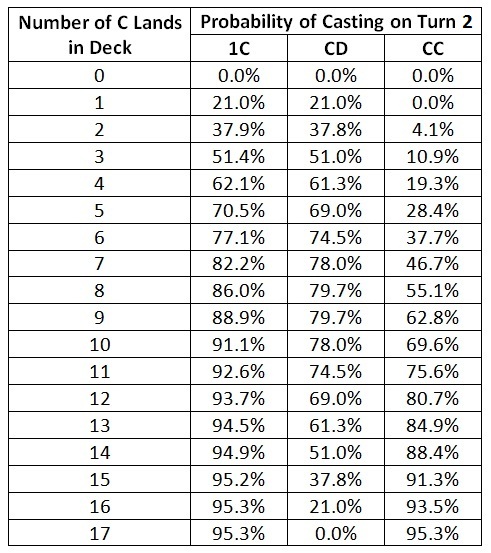
Do these numbers make sense? Let’s check the entries that can be verified without a calculator.
If the deck contains zero C lands, it’s impossible to pay any of the costs. The table correctly lists those probabilities as zero.
With one C land, it’s still impossible to pay CC. Again the table is accurate. Also, with one C land, in any situation where I can pay 1C, I can also pay CD. The table correctly lists those probabilities as equal.
With seventeen C lands in the deck, there are zero D lands. It’s thus impossible to pay the CD cost. The table correctly lists zero probability for that case. Furthermore, with no D lands to get in the way, in any situation where I can pay 1C, I can also pay CC. The table correctly lists those probabilities as equal.
The probability of being able to pay 1C is listed as the same for decks with sixteen and seventeen C lands. That’s because in both cases, any two lands from the deck will pay the cost. The table is correct that the chances are equal.
Finally, for the CD cost, the probabilities on the top half of the table should be the same but in reverse order to those on the bottom half. For example, it doesn’t make a difference whether my deck contains 5 C lands and 12 D lands or contains 12 C lands and 5 D lands. The probability for those two cases is equal. Indeed, they are listed so in the table.
To give a better understanding of what’s going on with the numbers, here’s a graph of the probabilities for the CD and CC costs.
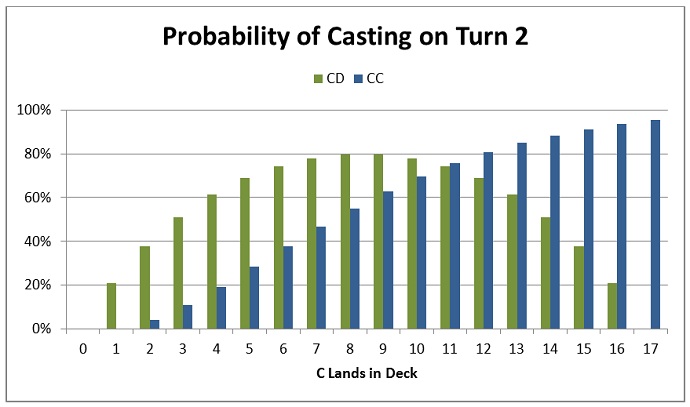
As expected, the chance of being able to pay CC increases with the number of C lands, the highest probability coming from a mono-colored deck. The chance of being able to pay CD is highest when the land split is most even. It falls off as the split becomes less even.
What can we learn from the graph?
The probability of casting CD and CC spells cross at eleven lands. In a deck with eleven Plains and six Forests, Vitu-Ghazi Guildmage and Precinct Captain have equal chance of being cast. With any more Plains, Precinct Captain is easier to cast. With any less, the Guildmage is the easier of the two.
Another interesting observation is that gold cards push me towards even land splits. The more evenly split my lands, the easier my gold cards are to cast. Their ease of casting falls off slowly as I move away from the middle of the graph. The falloff becomes more rapid as I cross the six to eleven ratio. In a deck that contains a substantial number of gold cards, it’s probably not wise to play a land ratio more asymmetric than six to eleven.
A final point of note is that the probability of casting Precinct Captain drops very rapidly as the number of Plains goes below eight. Below six Plains, the chance of casting the Captain on turn 2 is less than one in three. Given that Precinct Captain is strongest in the early game, I shouldn’t include him in my deck at those land ratios.
To complete the analysis, here’s a table for the three-cost spells.
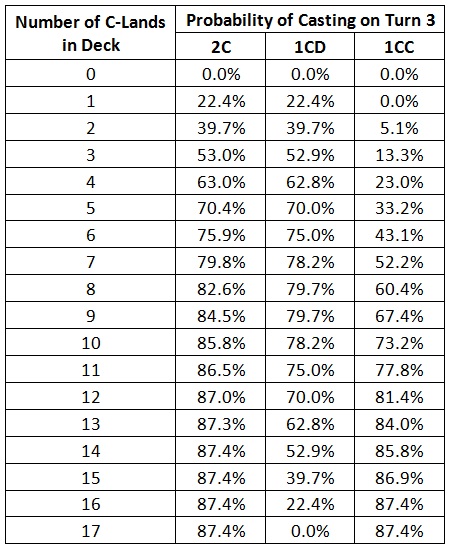
Here are the probabilities for the 1CD and 1CC costs in a graph.
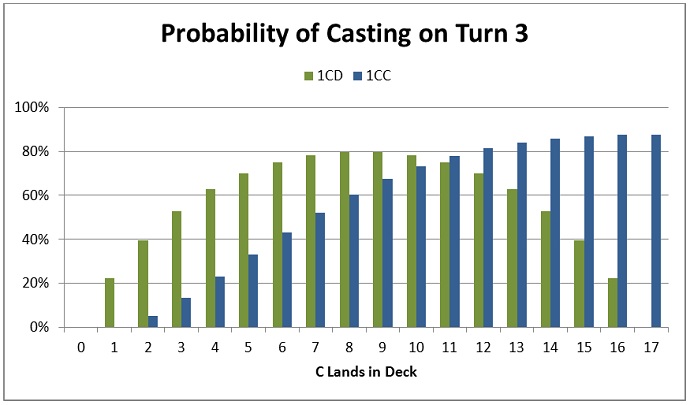
This graph shows the same basic patterns as the graph for two-cost spells. Again, the crossover occurs at eleven lands. Sunspire Griffin and Lyev Skyknight are equally castable in a deck with an eleven to six mana ratio.
Mulligans
It’s worth noting that I’m not accounting for mulligans. Throughout the analysis, I simply keep the first seven cards drawn. What does that mean for my results? It means that the percentages I give aren’t the true odds during play. Mulligans improve my chance of casting the spells. They slightly increase each listed percentage. The overall relationship between the percentages, however, will remain. The core conclusions, such as that CD spells are only slightly harder to cast than 1C spells, remain valid.
Deck Thinning
Gatecreeper is awesome. It fixes my mana now and gains me life later by chump blocking. It also does one other very minor thing: it thins my deck. It reduces my chance of drawing land later in the game when I’d much rather be drawing spells.
Of course, that effect is very minor. It’s more pronounced with Seek the Horizon. (For Mana Severance it’s very pronounced, but that’s not very relevant to Return to Ravnica Draft.) How small is the effect with Seek the Horizon? Is it an additional reason to play the spell, or is the effect so small that I should not consider it? Let’s find out.
I assume I cast each card on the turn corresponding to its casting cost and that the game ends during my tenth turn. For simplicity, I assume a four-mana starting hand. How many additional spells will I draw before the end of the game, on average, comparing games where I cast my deck thinning spell against games where I don’t?
I’ll do the calculation for Gatecreeper and for Seek the Horizon. Just for kicks, I’ve added in Mana Severance and a fetchland (Arid Mesa).
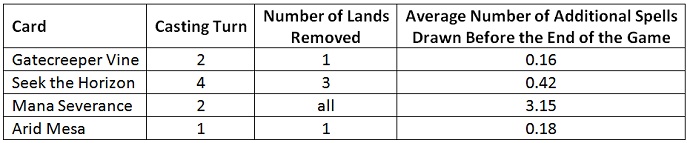
Not surprisingly, the effect for Gatecreeper Vine is small. I should play it for its great fixing, not for deck thinning. With Seek the Horizon, the effect is a nice bonus. In two of every five games I cast Seek the Horizon, I’ll get an extra spell out of the deal.
Takeaways
In a deck with mana sources evenly split between two colors, gold cards requiring two colored mana are nearly as easy to cast as mono-colored spells requiring a single colored mana.
Splitting your land evenly between colors makes gold cards easier to cast. Tend towards an even split if your deck contains a large number of gold spells. However, the detrimental effect of an uneven spilt doesn’t become large until you go beyond an eleven to six ratio.
At an eleven to six land split, it’s as hard to cast gold spells requiring two colored mana as it is to cast mono-colored spells requiring two colored mana. For land splits that are closer to equal, gold spells are the easier of the two to cast. For splits that are less equal, gold spells are the harder of the two to cast.
In almost half the games in which you cast Seek the Horizon early, it will cause you to draw one additional spell over the course of the game. The deck thinning effect of Gatecreeper Vine, however, is insignificant.
[email protected]
@DanRLN on Twitter
source code for the Magic Probability Toolkit
