Let us begin with a quick question.
Assume there is a four person, two round, single elimination tournament, and that the players break down thusly:
Rock,
Rock,
Paper, and
Scissors
(In case you never learned this on the playground, Rock smashes Scissors, Scissors cut Paper, and Paper covers Rock.)
Given that there are two copies of Rock, and remembering that there are two Rocks, which of Rock, Paper, and Scissors is most likely to win this four person, two round, single elimination tournament?
(This is not a trick question).
Go on…
Which is it?
Here be spoiler space…
Here be more spoiler space…
What about that Presidential election?
Who will win Game Seven?
Will the Celtics be the first team in NBA history to win a title without ever winning a single game on the road? (Probably not.)
How about religion?
…
I’m giving you room for your answer, in case you didn’t realize it…
Remember:
Rock,
Rock,
Paper, and
Scissors…
That is two (2) Rocks, one (1) Paper, and (1) Scissors.
This is not a trick question.
…
…
…
You said Rock, didn’t you?
“Good old Rock; nothing beats Rock.” -Bart Simpson

Except Paper.
Most people would glance at the above and assume that Rock wins half the time, Paper wins a quarter of the time, and Scissors wins a quarter of the time. The sad thing is, “most people” don’t even have the proper denominator. In fact, the four person tournament can only break down three ways:
Rock1 versus Rock2; Rock (doesn’t matter which)
Paper versus Scissors; Scissors
Rock over Scissors
Rock1 versus Paper; Paper
Rock2 versus Scissors; Rock
Paper over Rock
And
Rock1 versus Scissors; Rock
Rock2 versus Paper; Paper
Paper over Rock
So Paper wins 2/3 of the time, Rock wins 1/3 of the time, and given the constraints of our tournament, Scissors never, ever, wins. Never. Ever.
Wait a second! you might ask. Why are we doing this anyway? Why are there two copies of Rock in this hypothetical?
Believe it or not, this is probably the most useful article you will ever read about how to select a deck! Not a specific deck, maybe, but the process by which you can correctly, mathematically, select a deck! Really! And for the rest of your life!
From the dawn of Internet strategy posts and articles, from the earliest days of metagaming in Magic, our world has broken down into generalizations of Rock, Paper, and Scissors. The original R/P/S was Necropotence, U/W Control, and G/W Armageddon, with U/W over G/W and Necropotence over U/W; the problem is that as time went on the Necropotence decks got better, and more of the best players played Necropotence, and they added Land Tax to the Restricted List, meaning that this wasn’t much of a Rock-Paper-Scissors because Rock tore right through paper like it was, you know, soggy paper.
The other reason this wasn’t the best place for us to grow from is that it is potentially harmful to your mental game. I remember sitting down at my first Pro Tour next to my roommate Worth Wollpert. We had a B/R Necropotence deck (the same deck that Chris Pikula used to make Top 4 of that Pro Tour); Worth had an easy White Weenie matchup; I got Paul McCabe. We were all carrying two losses. Armed with both Black and Red removal in a deck full of Protection from White, Worth tore his White Weenie opponent in half… Did I mention I got Paul McCabe? I actually had a wicked start with first turn Hypnotic Specter, but Paul drew Necropotence first, recovered, and dispatched me in a tight one. Worth swung and slugged to Top 16, and McCabe, for his part, didn’t lose another game the rest of the Swiss and, as you probably know, won the whole Pro Tour with his Ihsan’s Shades and Sengir Vampires.
“Don’t you know by now that this game is all about matchups?”
I think Worth was trying to make me feel better, but I am pretty sure I went on tilt and threw my deck across the room at that point instead.
The fact is, this game is mostly about matchups; the problem is that this empowers us rather than enervating us, but that’s not how most people treat the information. Given a (real) Rock-Paper-Scissors metagame, many and most will see a world with no edge… By definition, all the decks are the same, 33.33% across the board. The truth, though, is that one of the decks will be more popular. It might not be “better” but people just like it more; otherwise, why would U/G Madness have been more popular than Psychatog in Standard? For illustrative purposes, we are calling that the double Rock in the four person tournament. But no one really plays in four person tournaments. Let’s jump – with the same proportions – from four to eight. Let’s call it…
Angelina,
Blake,
Charlize,
Drew,
Eva,
Fergie,
Gwen, and
Hayden
… with Angelina, Blake, Charlize, and Drew all Rock; Eva and Fergie Paper; Gwen and Hayden Scissors. By my count – and I did this by hand because I am a too few many years out of stats class to know the proper math, sorry – I got 105 possible first round matchups. What does this mean?
If you want to spend a couple hours laying all 105 (or more?) matchups out (like I did), you will find a lot of configurations that look pretty similar, say…
Rock versus Rock
Rock versus Paper
Rock versus Scissors
Paper versus Scissors
And
Rock versus Rock
Rock versus Paper
Rock versus Scissors
Paper versus Scissors
But in one of those Eva wins, and in the opposite Fergie does.
At the end of the 105 (that I ran), my handy dandy pivot table tells me that with thirty-five times the number of options, Scissors jumps, infinitely, from no chance whatsoever of winning to 12/105 (or a little over one-in-ten), Rock grabs twenty-eight (a little over one-in-four), and Paper – with the same number of entries as Scissors, mind you – nabs sixty-five, or over sixty percent of the available sixteen player tournaments!
Of course, most tournaments are not exactly sixteen players represented by exactly three decks in exact 1/2, 1/4, 1/4 proportion that fall one way or another 100% of the time, but again, this is done for illustrative purposes.
All in all, this has been a longwinded way of saying that which deck is actually favored to perform in a tournament might not be which deck conventional wisdom dictates. Like the title indicates, getting past this part is only the most basic test of metagaming competence. What is more important is that you actually pick the right deck to attack that metagame.
One of the problems with picking the correct deck is that most of our data comes from Top 8 deck lists reported on MagictheGathering.com or other sites, rather than the entire tournament; worse yet, many people took Frank Karsten’s popularity rankings as the actual popularity of decks in the metagame (Frank was actually going more for the intensity of the success of a deck… which is kind of the opposite, but not really). In our generalized three deck metagame, as time went by, Paper would be off the charts in the popularity rankings despite the fact that it is no more or less popular than Scissors in terms of the actual proportion of decks that you will likely play in the Swiss rounds. Put another way, conventional wisdom used to say that decks rise to Top 8 more-or-less in proportion to their populations in the Swiss… and then the Top 8 players battle it out; if Team ABU and New York States 2005 didn’t tell you otherwise already, now you know at least a simplified model as to why conventional “wisdom” proves once again to be a misnomer.
So say you are restricted to playing Rock, Paper, or Scissors only in a format where Rock is twice as popular as Paper or Scissors. Which deck should you play?
It’s pretty obvious, right?
That’s right… Scissors!
Well, that probably wasn’t so obvious. In fact, if you just want to “make Top 8,” the answer is almost certainly Paper. However, with a certain number of rounds, an interesting thing happens…
Paper is the New Rock.
Huh?
I can’t pretend to have run all the possible iterations of this scenario, but I have run it half a dozen times, and I got very similar results every time. I stretched from four to eight to two hundred fifty-six players. I ordered the 256 Rock (Rock), Paper, and Scissors representatives via random number generator and ran a single elimination tournament. And then I did it again. And again. Something very interesting occurred. Consider these charts and graphs:
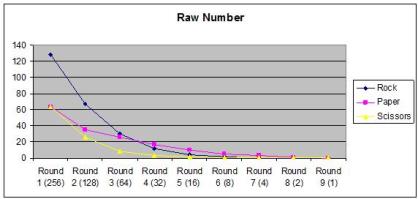
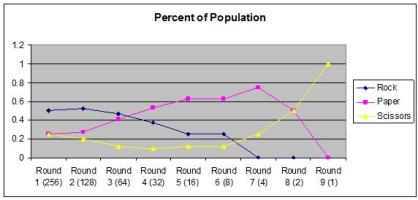
By Round 4 there are more copies of Paper than Rock in the tournament, and by Round 5, there are more than twice as many; Scissors is in single digits by Round 3, and by Round 6, a lone member of the Scissors clan is battling elimination round after round like Mark Herberholz at Table 1 in Philadelphia against Gadiel, Kai, Fujita, and Olivier Ruel, bruised and battered but Top 8.
So now you are in that sixth round, the Top 8 of our tournament. The breakdown at this point is…
Rock
Rock
Paper
Paper
Paper
Paper
Paper
Scissors
From this spot, everything is coming up Piznarski for Scissors. Scissors is 5/7 likely to not hit Rock, and the absolute worst case scenario is a Rock versus Rock matchup where only one Rock remains the next round. It is much more likely for Rock to fight Paper twice (which is what happened in the present scenario), giving Scissors a veritable Geoffrey Siron path to the title from three rounds out.
So the conclusion is…
The deck to make Top 8 is almost certainly a different deck than the one that you want to actually win the tournament. It has been said a couple of times – I think Osyp was the first one to mention it, when comparing U/G Madness to Affinity in Extended – that the Swiss rounds of a PTQ are essentially a different tournament than the Top 8, and the two will very often have completely different metagame proportions. Put a different way, Zvi and I once spent an afternoon discussing how often “the best deck” actually won the Pro Tour… I’ll leave our conclusions for another time.
The Case for Scissors
So how much do you want to gamble?
The PTQ player is presented with a serious dilemma, which I’m sure you understand at this point in the article… I resolved my opinion on it some years ago, after making innumerable Top 8s and not actually qualifying one too many times. I stopped playing decks that had nothing more to offer than good batting averages in the Swiss (like, say, Extended Doran) and resolved only to play decks that I thought could or would actually win a PTQ once in Top 8 position (however difficult is was to get there). Some member of Team Scissors seems to do well in the 256 player tournaments so long as one survives to the Top 8 (often you will see six Paper and one of each of the other two). The scary part for the potential Scissors mage is that just as often, sixty-three of the Scissors cohort are out of the running, and quickly. Then again, 255/256 magicians are not going to go home happy, anyway.
Most of the past and present members of the Apprentice program think that the framework that comes out of this way of looking at the metagame is the bee’s knees; approaching deck selection given the tools that come from this model are what helped position Two-Headed Giant’s deck setup in Charleston, allowed us to dominate more than one State Championships, put Josh Ravitz on the gravy train, and ultimately catapulted Steve Sadin from good PTQ player to very good PT player.
That said, this article covers only the most basic first step of the model. Given that I’ve spent most of my writing career trying to defy the notion of a no options Rock-Paper-Scissors framework and the design of rogue decks, there is obviously a set or two of additional steps, most notably:
1) Gwen or Hayden… How to Make Sure Your Scissors is the Scissors in the Top 8, and
2) Dynamite!
Another time for those.
LOVE
MIKE

