Dealing 3 damage is worth more than gaining 3 life.
You want to wait to chump block as long as possible.
Once you’re at an arbitrarily large life total, it no longer matters how much it is exactly.
These are all accepted truths about Magic. There is one theory behind life totals that gives a unified explanation for each of these strategic phenomena. You see, there are two ways to view individual life points. The most rigid and “logical” viewpoint is that each life point is worth the same as the next, as we all start with 20 and all die at 0. The other viewpoint goes a little beyond that abrupt definition by examining each life point as a separate, individual unit. Are you ready for the thesis? I think you are.
There is an inverse correlation between the number of life points a person has, and the value of the individual life point. That is, the more life you have, the less valuable each one is.
Now, before I begin, I want to announce the assumptions being made to deter nitpickers so I don’t have to do it throughout the article and disrupt the flow of the piece. First of all, there are always situations where the opposite of any accepted truth is accurate. Yes, you could be playing combo in a field of Burn and want to start at 23 instead of with them at 17. There are always hypothetical situations where a seemingly bad card can be the key to victory, and if you tried hard enough, you could find it for just about everything. None of that has anything to do with this article. Instead of coming up with scenarios where the accepted truth is incorrect, you should be learning about why the accepted truth is as such. If you must, imagine the entire article takes place between two evenly matched midrangish Limited decks between two players of equal skill level. Obviously the applications are far beyond that overly simplified scenario, but I just wanted to get this out of the way before diving head-first into the body of the article.
There are a few ways to go about this: Show a Repeat, Re-show Pete, or Jokes. Or I could just give you an example of the extreme and show how we can extrapolate that data into a much more relatable scenario.
When you are at four hundred seventy two billion, three hundred forty eight million, seven hundred ninety one thousand, six hundred thirty two, then the four hundred seventy two billion, three hundred forty eight million, seven hundred ninety one thousand, six hundred thirty third life point is as close to worthless as is possible without being literally worthless. But what about when you are at three? The fourth life point is pretty important now. That same one life means quite a bit to you all of the sudden.
What does that tell us? That the 4th life point is worth a great deal more than the 472,348,791,633rd, which means that the same must be true for, say, the 13th and 14th life points. Just on a much, much smaller scale.
Let’s do another example. Say you are going to play in a tournament where you get a bonus for your rating or whatever. Instead of byes, like at a Grand Prix, you get to start each game with a life advantage. Would you rather start at 23 or have them start at 17? The answer, quite obviously, is having them start at 17.
But why is that? Three life is three life, and it’s actually a lot easier to deal damage than gain life, so why would we have 17-20 advantage instead of 20-23 advantage? The reason is because their life is more valuable. I’ve heard similar things to this in the past, and it has become somewhat of a classic Magic riddle, if you will. The general consensus is that 17-20 advantage is better, but as far as I know, it hasn’t been properly laid out and explained in detail. The reason that the correct answer is 17-20 is because their 20th, 19th, and 18th life points are respectively more valuable than your 21st, 22nd, and 23rd. This is because of the inverse correlation of life total and the value of an individual life point.
Time for a third example. I’ve given you the extremes to show you that the theory holds true on the biggest of scales. I’ve given you a simple and relatable example that shows a hypothetical situation where the concept can be applied. Now I am going to get you to draw an imaginary graph. Then I’m going to give you an example that has nothing to do with Magic. Then a final example that is accessible and really ties the idea together.
I’m sure I could just use Paint and slap a makeshift graph into the article, but I think it’s better that you can visualize it. Actually, scratch that. I’ll just draw it.
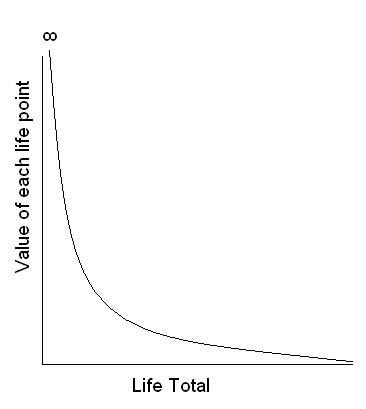
As you can see, your 1st life point is infinitely valuable. It’s like your King in chess. You lose if you lose that life point, so it has to have an in-game value of infinity. On the other side, you have a total approaching 0 while never actually being 0 until it hits infinity.
Poker is related to Magic fairly often, and I am going to do so now. If you are one of those people that doesn’t see the similar skill-set, avert your eyes. In tournament play, your chips are a lot like your life points in Magic. As you gain more, the less valuable each one is. This is one of the reasons that it is not right to take a favorable flip early in a tournament. Even if you are 55% to win the hand and double-up, the extra chips aren’t worth enough to overcome that 10% advantage you have in the hand. The chips you are risking are worth far more than the chips you are trying to win. This is the equivalent of sitting down for a multi-player game and flipping a coin with someone where one person dies on turn 0 and the other player starts at 40. The extra 20 life is worth less than the 20 you are risking, so it’s not worth the odds you are getting. Another parallel is that the difference between 90 and 91 big blinds is far less valuable than the difference between 10 and 11 big blinds. Sound familiar?
Speaking of Poker and Magic, how about that David Williams? What a master.
There is no quantifiable way of looking at the value of a life. Some opponents of my work with Stock Mana have made the argument that it doesn’t account for damage well enough. Guess what? Neither does anything else! Card advantage and number of interactions and so on all have no precedent about life totals. That is because life doesn’t have a rigid mathematical value. The value of each life can only really be figured out in context with one-another, and even then, it’s too dynamic of a resource to simply label with a number.
If your brain likes numbers, then I’ll give you an example of what it would look like if it was possible to label it. To be clear, this is purely a model to portray the concept.
c/n = the value of each of your life points, where n is the number of life points you have and c is the predetermined and somewhat arbitrary value of your first life point.
Let’s say that c is 1. That means that the first life point is worth 1 “value unit.” The second is worth .5 “value units.” The third is worth .33333 “value units,” the fourth is worth .25 “value units,” and so on.
To apply the mathematical model to my previous example, if you got to choose whether you start at 23 or they start at 17, here’s what you would do with c being 1:
1/21 + 1/22 + 1/23 = ~.0476 + ~.0454 + ~.0435 = ~.1365
1/20 + 1/19 + 1/18 = .05 + ~.0526 + ~.0555 = ~.1582
So what I did there was add the value of your 21st life, the 22nd life, and the 23rd life together and got about .1365 “value units”. Then I added up the value of the 20th, 19th, and 18th life points (in this case, your opponent’s), and as you can plainly see, .1365 < .1582, therefore the 3 damage that would be dealt is more valuable than the 3 life that would be gained.
(The reason that your life points and their life points can be compared directly and are interchangeable in the calculation is because you both start with the same amount, both die at 0, and it’s a two-person, zero-sum game, so the life totals correlate evenly)
That’s a mathematical explanation of the concept. The problem is that these “value units” don’t actually exist. The reason is that 1 life is not c/n where n is 1 and c is 1. In the model, c is essentially an arbitrarily chosen constant for the model to leap off of. Maybe you decide you want your model to be out of 100 because that makes more sense to you than using decimals. Voila! Just like that, c is 100. The metric unit of measurement is made-up.
The reason that the model isn’t actually applicable is because c is not 1, nor is it 100. In reality, c is infinity. Why? Because your first life total is infinitely valuable. This is true due to the fact that, in the game, nothing else matters whatsoever if you no longer have that 1 life point. Once you hit 0, you lose. At that point it doesn’t matter if your cards catch fire or if the table turns into a unicorn, busts through the ceiling and gores your entire family before doing a jig in the street on two hooves while the apocalypse rains down on the earth. Nothing matters anymore.
Using infinity, the model works for both of those values:
∞/0 = burnt cards, gored family, dancing unicorn, world explodes
∞/1 = ∞
That is when the model falls apart. It didn’t get very far in the real world, did it? Tis a shame.
The problem is that there is no “half of infinity.” Infinity divided however you want is still just infinity. So to get something that isn’t just infinity across the board, you would have to write it as c/n. To get something that gave actual definitions of what the value is in a way that accurately depicts the life totals, the only sensible thing to do is write it as ∞/n, which is worthless as a mathematical function beyond 1 life. That leaves us with the only option being to understand the concept through the multiple examples, mathematical explanations, and my artistically crafted graph, and use that knowledge to make assumptions pertaining to the value of a life point in context (of one-another, as well as the more complex yet common factors such as format and gamestate, but that’s a discussion for another article*). The important thing is to remember that each life point is worth more as you have less.
* In fact, Paulo recently wrote an article about chump blocking that talks about the format aspect of this, and I believe it should be mandatory reading in public schools. Get on it. As for the gamestate aspect, that is the stuff like “It doesn’t matter if you’re at 2 or 3 if they have a Sphinx of Jwar Isle that you can’t stop” and so on.
The model actually holds if you take a couple of out-there things as assumed. First, that infinity is a number rather than a giant blob of mathematical philosophy. Second, that whatever number you assign as c is capable of being a representation of what infinity would be if it were a number. You see, c is just a metric being used so we have something to measure the value against. Even if we take it as assumed that infinity is a number, nobody has any frame of reference whatsoever on what that number is, so in creating that metric by applying a known quantity to c and having it be representative of infinity, we make it so our output is quantifiable. Without c, each value would just be fractions of the number “infinity.”
So in this new, abstract, and entirely hypothetical universe I just created, infinity is a number rather than a concept, and 1 properly represents that number. Any fraction therein is merely a fraction of the number that infinity is.
Get it? Didn’t think so. The truth is that it doesn’t matter. Calculating the exact value in game is irrelevant. A lot of people seem to think that is the point of theory, when it is not at all. It is important to understand the concept and some basic principles of it, how to apply it, what its limitations and capabilities are, and so on. The fact that you have to jump through a bunch of hoops to get actual quantifiable data in this case is irrelevant since you aren’t going to sit there in a game and do the math anyway. This paragraph is just a preemptive strike at the naysayers who say that everything I am saying is useless because it doesn’t spit out numbers that play the game for them. Back to the version of the article where I’m not overly defensive and borderline resentful towards the public.
Time for the last example. This one is like the extremes one at the beginning of the article, but on a much smaller scale and the “extreme” part isn’t the starting life totals, but rather the amount of life being gained. Ready? Break!
You would rather gain 9 life while at 1 than gain 10 life while at 10.
If the value of a life was rigid, this statement would be absurd; 10 life is one more life than 9 life! The fact that this statement is true, and true to the point that I doubt anyone even batted an eye when considering it, is proof of the thesis of this article. Let’s break out the model that I just told you not to use and use it.
c/n = value, n is life total, c is 1
1/11 + 1/12 + 1/13 and so on to 1/20 = ~.669
1/2 + 1/3 + 1/4 and so on to 1/10 = ~1.929
So going from 1 to 10 is almost 3 times as valuable as going from 10 to 20 despite the fact that it is actually less life.
Some interesting food for thought, no? This explains a few things (many of which have alternative explanations in addition to this theory being applied, which I will note when appropriate).
First of all, why chumping as late as possible is optimal. In addition to giving you more options depending on what cards you draw, it is also because saving 3 life while you’re at 7 is more valuable than saving 3 life while at 18. That value could be due to the extra options you gain by waiting, but then we get into a chicken and the egg ordeal instead of appreciating the strategic ramifications.
It explains why painlands seem a lot less painful during the first few turns. With a Ravnica dual, or “shockland,” a player will often go to 18 to cast their spell on time, but may choose to wait for their six-drop for a turn, opting to play the land tapped when at a lower life total, for instance, 5. That is because those last few life points are far more precious than the first couple. Again, it could be because jockeying for position earlier in the game is important because whoever is ahead gets more of an advantage the more time they are ahead, but who’s to say that isn’t one of the reasons the first few life points don’t matter as much? Chicken versus Egg, etc.
It also explains why cards can gain upwards to 8 life for 1 or 2 mana but a card can only dome for 3 damage for the same investment. Look at Lone Missionary; do you think a 2/1 for 1R that domes them for 4 could realistically be printed? Despite the fact gaining life is actually the more scarce effect and the life swings are higher, direct damage is far more prevalent than straight life gain throughout all of Magic.
All of this and more can be explained by the inverse correlation between the number of life points a person has, and the value of the individual life point. Thanks for reading.
Next week I have some talk about the new Limited format and some classic AJ rants. I was going to post that this week and this next week, but technical difficulties forced me to flip them. I would, however, like to take the time to thank some people.
Sadin — Thanks for putting me up while I was in town.
Kathryn — Thanks for letting me crash, it was great seeing you.
Camila — It was great meeting you, you’re awesome. Thanks for putting up with me invading your sanctuary.
Martel and Jon — Thanks for hosting drafts.
Everyone I got to see/hang out with/meet/be near in New York — You guys are awesome.
Jerret and Calosso and everyone I borrow stuff from in real life — Thank you for enabling a lazy cheapskate. It wouldn’t be possible without you. Hopefully some of you are in Atlanta this weekend or I’m just doing ggslive coverage.

