I was playing Magic Online the other day, and trying to decide if I should do a 4-3-2-2 draft or an 8-4. I ended up picking a 4-3-2-2, just because it looked like the 8-4 would be a while before starting, but it got me thinking about the sort of conventional wisdom that people deliver about picking between the two.
“They” say that the 4-3-2-2 queues are a poor choice for any halfway decent player. They say that the payouts in the 4-3-2-2s are just not worth it, since They would like to get more for winning a draft than just the originally invested set plus one pack. I’ve even heard some members of Them who were playing in the 4-3-2-2s express outrage that they would face players with ratings at or near 1800, as such players belong in the 8-4 queues. As Stephen King once wrote, “They do like to talk, don’t They?”
Well, I am the sort of person who tends not to take Their word for it. A mathematical approach to this problem came to mind for me, and I thought I would apply it, because I’m just that sort of guy. The remainder of this article will demonstrate my results.
[Warning: as you might imagine, some mathematics are ahead, the sort which assume you have a pretty good grasp or algebra and such. If you don’t, remember your Back button.]
Let’s say W is the probability of you winning a draft match. There are no unintentional draws in a single-elimination draft, so your probability of losing is thus 1-W. In a 4-3-2-2 queue, your possible wins occur thusly (W^3 indicates “W to the third power”):
** You win 4 packs with probability W^3
** You win 3 packs with probability (W^2)*(1-W)
** You win 2 packs with probability W*(1-W)
** Otherwise, you get jack squat.
So, after some algebra your expected win is (W^3) + (W^2) + (2*W). Frankly, that doesn’t tell us a damn thing. There’s nothing useful we know about that function, except that it is minimized at zero. So, if your probability of winning a draft game — ever — is zero, then your winnings will be minimal. Good thing I’m around to tell you this stuff, eh?
But wait! If you go look at the DCI Floor Rules, you’ll find that the DCI needs to estimate each player’s probability of winning in order to calculate ratings. They do this with the following formula, where D is equal to (Opponent’s rating — Your rating):
W = 1 / ([10 ^ (D/400)] + 1)
Now we’re getting somewhere. If you plug that in for W, you get a really complicated function which nobody in their right mind would want to work with. Fortunately, there exists stuff like the Function Grapher Online that will do this work for us. It graphs the function and we get this graph, where the horizontal axis is the rating difference and the vertical axis is the expected number of packs won:
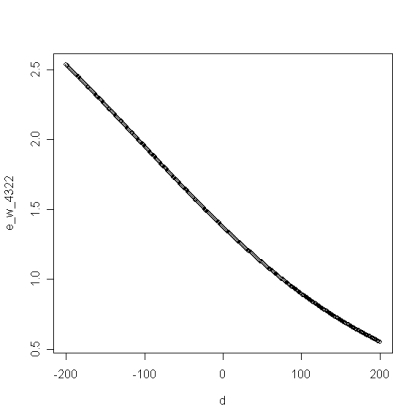
It seems that this actually confirms what They say. If you have a much higher rating than the opposition you are expecting (i.e., your D is negative by a big margin), your expected win goes up. If you are much lower rated than your opposition (D is way positive), then your expected win goes down. Thus, high-rated players expect to win more. Well, that why they’re higher rated, derf!
However, let’s compare with the 8-4 queues. This gets a little more complicated because there is the possibility that no game will be played in the final round, and both players will split for six packs each. Of course, not everybody actually splits. If the probability of a split is S, your results are then:
** You win 8 packs with probability (W^3)*(1-S)
** You win 4 packs with probability (W^2)*(1-W)*(1-S)
** You win 6 packs with probability (W^2)*S
Then some algebra gets us to an expected win of 4*(W^3)*(1-S) + 2*(W^2)*(S+2). Again, even with an estimate of W we can work with, trying to figure out how that function works doesn’t look like a lot of fun. To work with it, we’re going to have to make some assumptions about how often you might split in the finals of an 8-4.
So, let’s assume you split half of the times you make the finals — which seems like a very conservative estimate, since splits happen a lot more often online as far as I can tell. Then S=1/2 and we get a much simpler expected win function of 2*(W^3) + 5*(W^2). We plug in the ratings estimate of W again, and the handy-dandy Function Grapher gives us this:
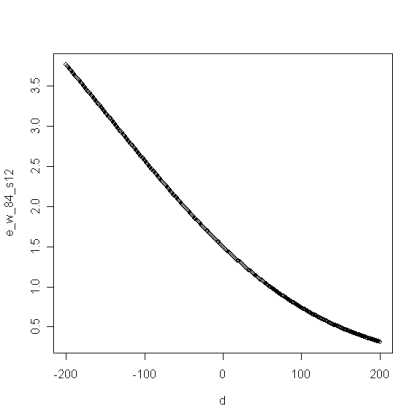
We get the same result, but it’s worth noting that the curve is steeper at the ends of the 8-4 queues; in other words, if you’re going to play somebody 200 points higher than you, you’d much rather be doing it in a 4-3-2-2 since your expected win is higher and the opponent’s expected win is lower. And if we assume that you split even more often than half the time, say S=3/4, we get more of the same:
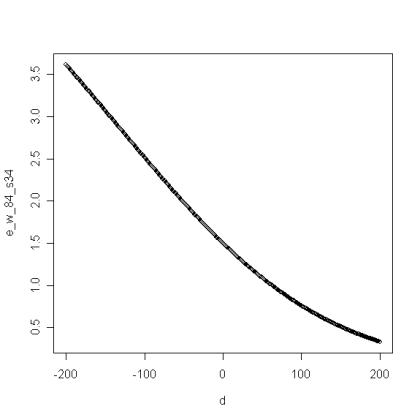
Implications and Conclusions
The above analysis suggests that in general, it’s bad to play any sanctioned draft if you are much lower-rated than your opposition. Of course, that’s not the line of thought that I am recommending you lower-rated folks out there take. If you let simple mathematics make you that pessimistic, you’re in some real trouble, since we’re all dead in the long run.
Instead, you first need to remember what is meant by “much higher” or “much lower” in terms of these graphs. If you look at those functions over the gap [-10, 10] or even [-50, 50], they’re pretty close to straight lines. There’s not much suffering or benefit to be had by playing people who are a little better or worse than you, or an individual person who’s much better or worse than you; the above graphs are calculated with the average rating of the rest of the entire tournament in mind. If you are rated 1600, sitting down at a draft table full of 1800 players is bad news, but having one 1800 player mixed in with several other players who are 1550-1650 is not so bad.
Also, you need to remember that everybody was low-rated once. A year and a half ago, Seth Manfield was doing okay for himself rating-wise — he had recently qualified for his first Pro Tour — but if you compared his rating to that of, say, Luis Scott-Vargas, Seth was still like a 1650 player at the 8-4 tables. Yet, with lots of practice against strong competition, Seth was able to ascend to the level of Grand Prix Champion last month, beating Scott-Vargas handily along the way.
It’s not that you shouldn’t try to get better by facing strong competition — by being the lone 1600 player at the 8-4 table, say — it’s just that you had better be willing to take some losses along the way. The math says it’s bound to happen, at least until you can rack up enough wins so that you are the higher-rated player. Better save up money for draft sets.
mmyoungster at aim dot com
mm_young dot livejournal dot com
mm_young on MTGO

