Limiting Chance is a series that uses mathematics and probability to investigate aspects of Limited play. In this article, I continue looking into the average casting turn of spells, a quantity I have dubbed "turn cost." I focus on the effect of colored mana on turn cost.
Colored Mana
We all know that colored mana in a spell’s casting cost makes that spell harder to cast. If I’m playing a two-color deck, about half the land in my deck can’t produce that spell’s color. So inevitably there will be times when I have the right amount of mana to cast the spell but not the right colors.
If a spell’s converted mana cost is large, a few colored mana aren’t going to make much of a difference. Once I’ve got enough mana to cast the spell, I’m fairly likely to have the color I need. Therefore, it seems that the relevant quantity is a spell’s ratio of colored mana over converted mana cost. If that ratio is high, the spell is harder to cast than you’d expect from its converted mana cost. If the ratio is low, the spell isn’t much harder to cast than a colorless spell of the same converted mana cost.
Is it possible to be more precise? Yes. I can use turn cost to measure the effect that colored mana has on how hard a spell is to cast. In a previous article, I defined the turn cost of a spell to be the average turn on which I am first able to cast that spell. Read that article for a longer introduction to the concept of turn cost and an argument for why it is an important and useful quantity to study.
Turn Cost
Three-Mana Spells
Let’s start by looking at the effect that colored mana has on the turn cost of three-mana spells.
For this calculation, I use a 40-card deck with 17 lands. The deck contains eight lands of one color, eight lands of a second color, and one dual land. I model the effect of mulligans using the technique described in this article. I use my standard mulligan goal of four spells and four lands by turn 4. Additionally, I mulligan any seven-card hand that does not contain at least one source of each color. All calculations are done both on the play and on the draw, and the results are averaged. You can download the source code for the calculations used in this article here.
I use the letter ‘C’ as the mana symbol of an unspecified color. I use the letter ‘D’ as the mana symbol of a color other than C. This is generally accepted notation.
For three-mana spells of various casting costs, here is the average turn on which the spell first becomes castable.
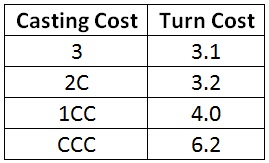
Not surprisingly, the more colored mana in the spell’s cost, the worse the turn cost. The first colored mana has almost no impact. A spell costing 2C is only very slightly slower to cast than a three-mana artifact. At two colored mana, the impact is significant. On average, I have to wait almost one turn longer to cast a 1CC spell. At CCC, the impact is severe. I have to wait almost twice as long to cast a spell costing CCC.
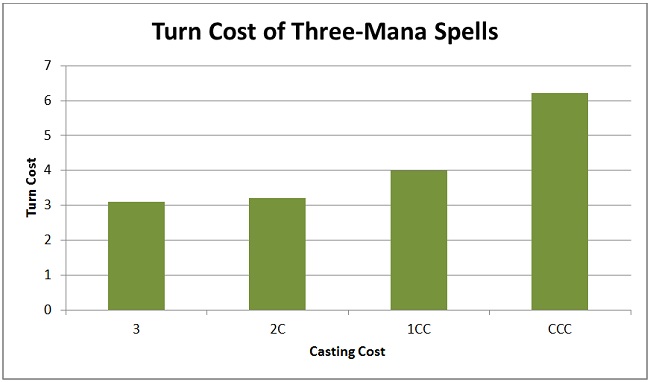
I find that visually representing trends in numbers makes those trends easier to grasp. Here is a graph of the turn costs.
Four-Mana Spells
Here are the turn costs of four-mana spells.
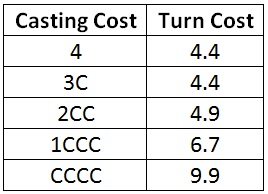
Again, the first colored mana is insignificant. Its effect doesn’t even show up in the first decimal place. Two colored mana forces me to wait on average half a turn longer. For CCCC, I have to wait a whopping five-and-a-half extra turns. With a turn cost of 9.9, it is harder to cast than a seven-mana artifact. (The turn costs of colorless spells can be found in the first table of my previous article.)
Five-Mana Spells
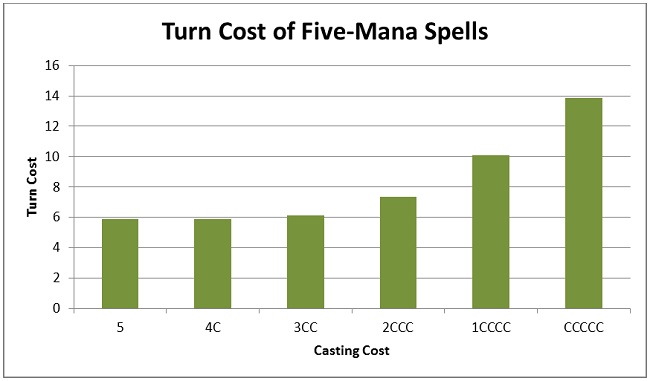
Five-mana spells are very forgiving of both the first and second colored mana.
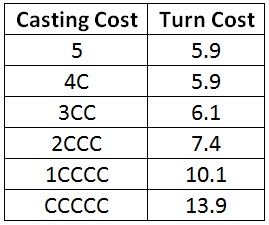
For lower casting costs, two colored mana had significant impact. However, at five, neither one nor two colored mana has much effect. I don’t need to worry until 2CCC, for which I’ll have to wait an extra turn-and-a-half. CCCCC clocks in at a turn cost of 13.9, which makes it equivalent to Colossus of Sardia, a nine-mana artifact. (A quick Gatherer search reveals that the only CCCCC card ever printed is Rushwood Elemental from Mercadian Masques.)
Six-Mana Spells
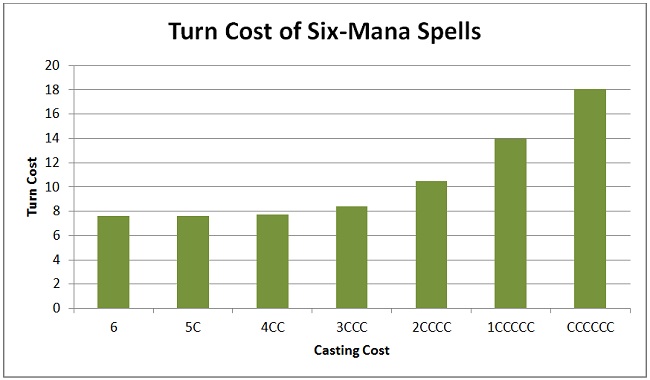
Six-mana spells are very similar to five-mana spells.
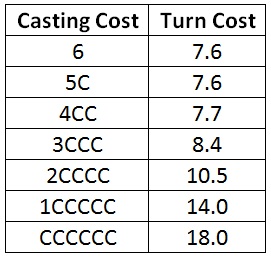
Again, both one and two colored mana have almost no effect on casting turn. Even three colored mana requires waiting less than one turn extra. (For those keeping score, Primalcrux is the only CCCCCC spell.)
One-Mana Spells
I started at three mana and went up. Now let’s jump down to one mana. Here are the casting turns of the two one-mana casting costs.
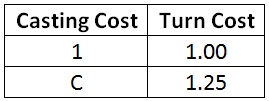
When I first saw the casting turn of a spell costing C, I was surprised by how high it is. Do I really have to wait an extra quarter turn just because the spell costs colored mana? Aren’t I very likely to have one mana of the appropriate color at the start of the game, especially considering that I am mulliganing seven-card hands that do not contain both colors? I took a closer look at the results.
It turns out that I am very likely to cast a spell costing C on turn 1. The probability of being able to cast it first turn is 92.6%. However, if I can’t cast it on turn 1, it’s probably going to take quite a while to find the color I need. On average, I will have to wait an extra 3.4 turns before I can cast the spell. (That is, until around turn 4 or 5.) A 7.4% chance of having to wait 3.4 turns corresponds to an extra one-fourth of a turn on average. (Multiply the probability by the number of turns to get that result.)
Two-Mana Spells
Experience tells me that double-colored two-mana spells have high variance. They are often very impressive two-drops, but if I don’t start with the correct mana, they can take depressingly long to cast. In that case, they are often irrelevant by the time they hit the table.
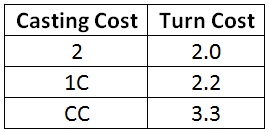
A single colored mana is not too big a deal, but CC spells require me to wait more than a full turn longer on average. Is this the high variance I was expecting? Let’s do the same analysis I did for one-mana spells.
The probability of casting my CC spell on turn 2 is 70.1%. The average extra wait when I can’t cast it on turn 2 is 4.2 turns. (That is, I will have to wait until about turn 6.) That matches with my experience of high variance. A reasonable chance of casting on turn 2, but a long wait if I can’t.
Casting Costs Ranked by Difficulty
When judging the relative power of two cards, it is important to be able to accurately compare their costs. For that purpose, I now expand my calculation to include all casting costs.
Here is a list of all reasonable casting costs ranked in order of their turn cost. This list includes gold cards.
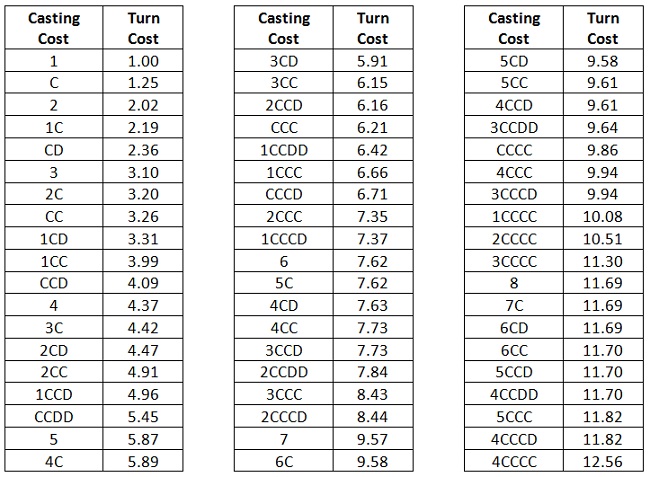
The most interesting cases are when a spell is more costly than another spell with a higher converted mana cost. Notable examples include:
- CC, which is harder to cast than 2C.
- CCC and 1CCC, which are harder to cast than 3CC.
I discussed this in greater detail in a previous article, but this table demonstrates that gold cards are easier to cast than one might naively expect.
- CD is somewhat harder to cast than 1C but is much easier to cast than CC.
- 1CD is very slightly harder to cast than 2C. It is much easier to cast than 1CC.
- 3CD is almost equivalent in turn cost to 4C.
- The same is true for 4CD and 5C.
For casting costs that I don’t have a lot of experience with, it can be useful to relate them to costs I know very well.
- CCDD is easier to cast than 4C but is harder to cast than 2CC. That is relevant when evaluating the power of some guild leaders.
- 2CCDD is only slightly harder to cast than 4CC. Again, this is relevant to guild leaders.
Hybrid Spells
Note that I can use the above table to evaluate hybrid cards as well. If my deck includes both of the hybrid card’s colors, I should treat the hybrid mana as colorless when using the table. If my deck has only one of the hybrid card’s two colors, I should count the hybrid mana as C mana.
Asymmetric Mana Base
Up until now, I have used a deck with eight sources of C mana, eight sources of D mana, and one dual land. In reality, my mana base is not always that symmetric. What effect does the asymmetry of my mana base have on casting turns? Specifically, let’s look first at how many C-lands I need to include in my deck so that a 1CC spell is as easy to cast as a 2D spell.
To model the effect of mulligans in this calculation, I no longer mulligan seven-card hands that are missing a color. That rule is not reasonable when the number of C or D sources in the deck is small. I use only my standard mulligan goal of four spells and four lands by turn 4.
Here is the casting turn of spells costing 1CC and 2D as I increase the number of C-lands in my deck. The total number of lands in the deck remains seventeen, with one of those being a dual land and the rest D-lands.
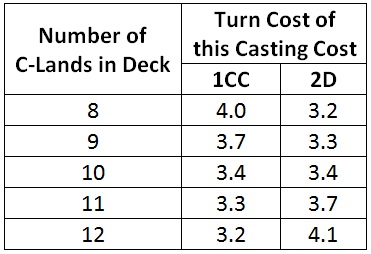
As expected, the turn cost of a 1CC spell drops as I add C-lands, and the turn cost of a 2D spell rises. The results are easier to see as a graph.
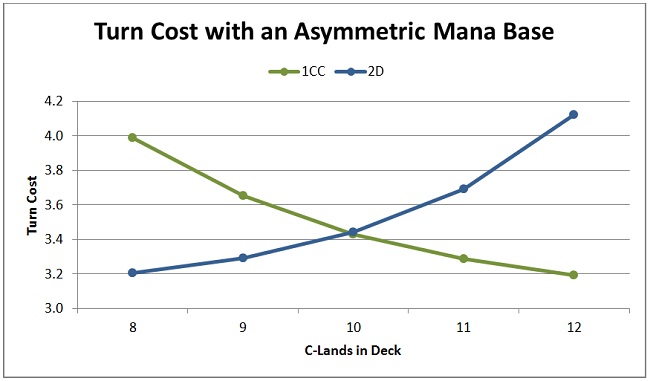
The casting turn of the two spells crosses at ten C-lands. That means when my deck contains ten C-lands, six D-lands, and one dual land that spells that cost 1CC and 2D are equally hard to cast.
Let’s expand the calculation to include other converted mana costs. I am interested to know if their crossover points occur at around the same number of C-lands. Here are the crossover points for various converted mana costs; the point when a spell with two colored mana in its cost has the same turn cost as a spell with a single colored mana in its cost.
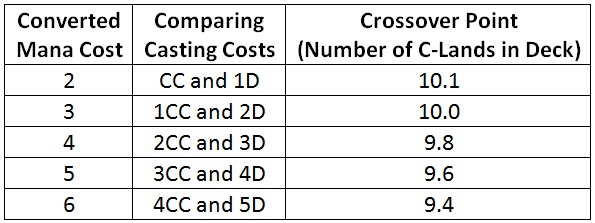
For all of the converted mana costs, the crossover occurs near ten C-lands. That means if I have a deck with an even split between C and D-colored spells, all of the C-color spells require two colored mana, and all of the D-color spells require only a single colored mana, I should use a mana base with ten C-lands.
That of course is a fairly unlikely scenario, but it gives a reasonable upper bound on the number of C-lands to include in my deck. Based on the actual number and color of spells costing two colored mana, I should choose a number of C-lands between eight and ten. I should only use a mana base more asymmetric than ten C-lands if I have a large number of spells with three colored mana in their cost or if the relative number of spells between the two colors is significantly asymmetric.
Splash
Splashing is common in Limited decks. When my card pool includes one or two powerful spells that aren’t in my deck’s main colors, I often look to include them in my deck. When I do, I only use a small number of sources of that color so as not to disrupt the core of my mana base.
Experience tells me that the best splash cards are often those with a high converted mana cost. If I do splash a low-cost spell, I need to make sure it’s relevant in the late game. That’s because, with a low number of on-color sources, I’ll very likely be waiting for that color before I can cast my splashed spell.
In terms of turn cost, I’m paying a premium for the splashed spell. How much is that premium, and how much does the number of sources affect that premium?
Number of Sources
Let’s look at the number of splashed mana sources first. For this calculation, I will splash a spell that costs 4C. How does the turn cost of the spell vary as I change the number of C mana sources in my deck?
I use my standard mulligan goal of four spells and four lands by turn 4.
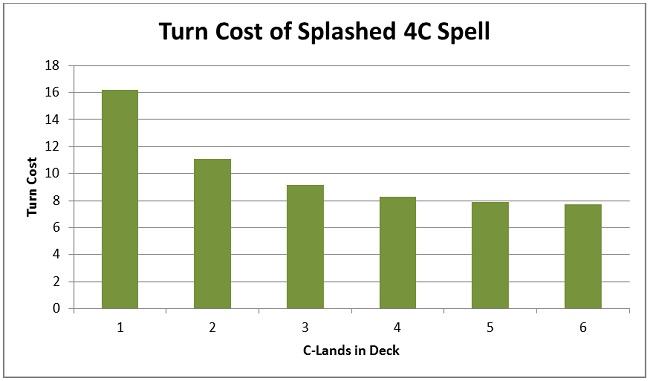
Here is how the turn cost of the 4C spell varies as I add C-lands to the deck.
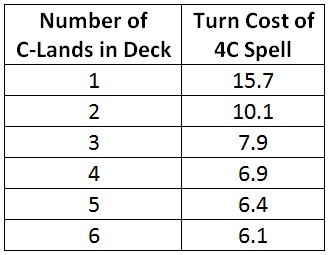
The turn cost falls off quickly for low land counts and then levels off. Beyond three or four C-lands, adding additional sources has diminishing returns. This indicates that three or perhaps four is the correct number of splashed mana sources to play.
Turn Cost Premium
Assuming I play three sources, how much of a turn cost premium do I pay for my splashed spells? What are their turn costs?
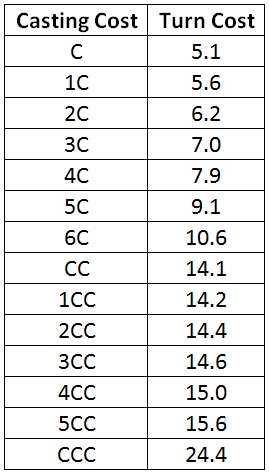
The turn cost of spells with two colored mana in their cost is prohibitive. Normally, a CC spell has a turn cost of 3.3. When splashed, the turn cost is 14.1. I don’t care how good that spell is. Fourteen turns is too long to wait. The cost of triple colored mana spells is laughable. Clearly, spells with more than one colored mana in their cost should not be splashed.
To better understand the premium I pay for splashing a spell, I can look at the difference in the turn cost between the splashed spell and the turn cost I usually pay for that spell.
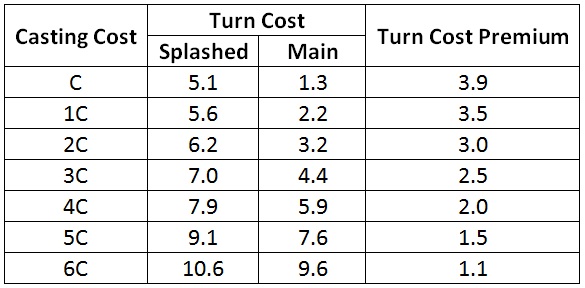
Notice how the premium drops as the spell’s converted mana cost increases. That’s because by the time I can cast a high-mana spell, I’m likely to have drawn one of my splashed sources. In general, high-mana spells are a safer bet when it comes to splashing.
Effective Mana Cost
One way I can express the premium I pay for splashed spells is to translate their turn cost into an effective mana cost. I do that by answering the following question. What D mana cost has the same turn cost as the splashed spell? (Here I use D to represent one of my deck’s main colors, while C is the color of the splashed spell.)
Obviously, the turn cost of the splashed spell is not going to correspond exactly to any D mana cost. The turn cost will fall between two mana costs. To determine the effective converted mana cost, I linearly interpolate between two surrounding D mana costs. For simplicity, I consider only D mana costs that include a single colored mana.
Here are the effective mana costs of splashed spells.
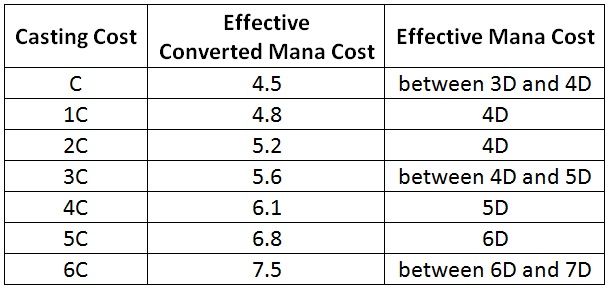
How do I read this table? As an example, the table is saying that when I am considering whether to splash a 1C spell, I should evaluate that spell as though it costs 4D. When I am considering whether to splash a 3C spell, I should evaluate that spell as though it costs somewhere between 4D and 5D.
Takeaways
For converted mana costs up to four, a single colored mana in the cost has no significant impact on what turn you can first cast the spell. A second colored mana does have an impact.
For converted mana costs five and six, two colored mana in the cost have no significant impact on what turn you can first cast the spell. A third colored mana does have an impact.
On average, you can cast spells costing 2C earlier than spells costing CC. You can cast spells costing 3CC earlier than spells costing CCC.
On average, you can cast spells costing CD earlier than spells costing CC. You can cast spells costing 1CD much earlier than spells costing 1CC.
In a deck with an asymmetric mana base of ten Forests, six Islands, and one Breeding Pool, spells with two green mana in their cost are just as easy to cast as spells of the same converted mana cost with just a single blue in their cost.
When splashing, include three or four mana sources of that color in your deck. Including less has a significant negative impact on when your splash color is likely to come online. Including more gives diminishing returns.
Do not splash spells with more than a single colored mana in their cost.
When you splash a spell with a low converted mana cost, expect to be able to cast it much later than you normally would. The lower the casting cost, the longer than normal you are likely to wait.
[email protected]
@DanRLN on Twitter
source code for the Magic Probability Toolkit
