Magic is an extremely fun game. It’s more fun than chess, and it’s more fun than poker. Why? Because it sits half way between those games, taking the best qualities from each. Magic is like poker, but it has a more complex game state and greater tactical depth. (You know, like chess.) And Magic is like chess, but with more variance and more hidden information. (You know, like poker.)

In this series, Limiting Chance, I’m going to focus on the aspects of Magic that draw from poker: the randomness.

In Magic, like with anything random, you can never know exactly what’s going to happen next. You make your best judgment with the limited information available, and then you hold your breath and hope things go your way. It creates tension. It creates excitement!

But I’m not playing only for fun and excitement. I’m playing to win. How does variance affect what I need to do to win? Instead of planning in terms of absolutes, like I can in chess, I’m forced think in probabilities, as with poker. I weigh the odds and make a decision based on what (I think) is most likely.

• Should I cast my bomb now? What are the odds my opponent’s got a counterspell?
• Should I use removal on that 2/2 flyer? What are the odds that next turn I’ll draw the one land I need to cast my Spider?
• Should I mulligan this two-land hand? What are the odds a six-card hand will be worse?

These are the kinds of questions I confront as a Magic player, and I can never know the "right" answer. I can only figure the odds and make the choice most likely to go in my favor. After that, if things don’t pan out, so be it. I did the best I could.

Or did I? How good am I at figuring out those odds? Well, top ranked Magic players are clearly very good. They have internalized a ton of probability. They may not be able to talk in terms of math and percentages, but they have played enough Magic to build up an intuition for the choices they make every game. They know the right answer in their gut, even if they can’t whip out a calculator and prove it.

Well, I want to take things one step beyond intuition. In poker, players are way past intuition. Any professional poker player knows the odds of winning or losing a given hand. They can look at the river, look at their hand, and know whether to fold. If you’ve watched poker on TV, you’ve seen that they put the odds on screen so you can follow along at home. Professional poker players take probability very seriously. They’ve done the math (or at least memorized the numbers) and use it in every decision they make.

There’s no reason I can’t do the same for Magic. I am going to take the mathematics of probability and apply it to the questions of Magic. I am going to arm myself and you with the same type of knowledge that professional poker players bring to their game.

And just so you know, I’m the right guy for this job. I’m an avid Magic player, so I know what decisions are critical and interesting. I’ve got a Ph.D. in quantum physics, so my understanding of probability is strong. And I earn my living programming video games, so I can build the tools needed to do the complex calculations.

Limited

I’m going to focus my investigations on Limited play. Why is that? Two reasons:

• I love Limited Magic. Draft is by far my favorite format, with Sealed coming in second. I play Constructed, but man do I love Limited.
• Constructed decks vary wildly, but Limited decks are all fairly similar. When I answer a question of probability for Limited, the answer is likely to be useful across a majority of decks. That’s not true for Constructed.

In Constructed there are a myriad of different decks with odd land counts, crazy ramp, weird combos, etc. Each deck plays differently, and there are fewer questions of probability that have a single answer for all decks. Most Limited decks, on the other hand, follow the same basic template. There is slight variation, but the Limited plan is almost universally to drop one land each turn, cast creatures, and curve out to overwhelm the opponent. That similarity between decks opens up a vast treasure trove of universal questions, questions that crop up time and time again in both the piloting and construction of Limited decks.

Now let’s see what questions we can answer about Magic by applying probability and mathematics!

How Many Lands?

I’m going to start things off with a simple question. How many lands can I expect to draw in my opening hand?

Not surprisingly, it depends on the number of lands I’m playing and the size of my deck. I know the size of my deck: 40 cards. It never makes sense to play more than 40 cards in a Limited deck. Playing more than 40 dilutes my card quality and increases my deck’s variance. I always play a 40-card deck.

It’s generally accepted that the correct number of lands to play in a 40-card deck is 17. There are many reasons I might increase or decrease that count, but the baseline is 17 lands. So I’ll assume I’m playing a deck with 40 cards and 17 lands. Unless I state otherwise, that’s the land count and deck size I use for all my calculations.

Now back to the question at hand. How many lands can I expect to draw in my opening hand?

One-Card Hand

When I draw my first card, there are 40 different cards I might draw. Of those 40, 17 are land. So my chance of getting a land on my first draw is 17 in 40. That’s the same as saying 17 divided by 40. Grabbing a calculator, I get:

17/40 = 43%

For a one-card hand, the chance that I have a land is 43%.

Two-Card Hand

Before we jump all the way up to a seven-card hand, let’s look at something simpler. Let’s look at a two-card hand. How many lands can I expect to draw in a two-card hand? There are four different things that can happen when I draw two cards. Here they are listed in a table.

Things That Could Happen	Number of Lands in My Hand
1) I draw a land, and then I draw a second land.	2
2) I draw a spell, and then I draw a second spell.	0
3) I draw a spell, and then I draw a land.	1
4) I draw a land, and then I draw a spell.	1

What is the chance of each of those possible outcomes? To determine that, I need to use the following fact about probability: the chance of two things happening is equal to the chance that the first thing happens multiplied by the chance that the second thing happens.

("probability of 1st thing") × ("probability of 2nd thing") = ("probability of both things happening")

Knowing that, I’ll go through each of the four possibilities.

1) We know the chance of drawing the first land is 17 in 40. After I draw that land, there are only 16 left in the library. Also, my library now only contains 39 cards. So the chance of drawing a second land is 16 in 39. That makes the chance of drawing a land twice:

17/40 x 16/39 = 17%

2) There are 23 spells in the deck, so the chance of drawing a spell on the first draw is 23 in 40. Once I’ve drawn a spell, the library is left with 22 spells. The chance of drawing a second spell is 22 in 39. That makes the chance of drawing zero lands:

23/40 x 22/39 = 33%

3) After I draw a land, all 23 of my spells are still in my library. So the chance of drawing a spell from the smaller library becomes slightly higher, 23 in 39. That makes the chance of drawing a land and then a spell:

17/40 x 23/39 = 25%

4) After I draw a spell, the chance of drawing a land is 17 in 39. So the chance of drawing a spell and then a land is:

23/40 x 17/39 = 25%

Here’s the same table as above, but I added a column for the probabilities I just calculated.

 

Things That Could Happen	Number of Lands in My Hand	Probability
1) I draw a land, and then I draw a second land.	2	17%
2) I draw a spell, and then I draw a second spell.	0	33%
3) I draw a spell, and then I draw a land.	1	25%
4) I draw a land, and then I draw a spell.	1	25%

In two of the four possible outcomes (3 and 4), I end up with a single land. To calculate the total chance of getting a single land, I add up the probability of those two outcomes. So the chance of drawing one land is:

25% + 25% = 50%

Now we know the chance for each possible land count in my two-card hand.

 

Number of Lands in My Two-Card Hand	Probability
0	33%
1	50%
2	17%

I’ve got a 50% chance of getting one land. I guess that’s ok, but I still don’t plan on mulling to two anytime soon.

Notice that the probabilities add up to 100%. Good! If they didn’t, it would mean that something is wrong with my math.

Seven-Card Hand

Of course, what I really care about is a seven-card hand. If you understood the process I used for a two-card hand, you also know how to figure out a seven-card hand. It takes all the same steps; it just takes a lot longer. With a seven-card hand, the table of things that could happen is 128 entries long!

So I wrote a computer program to do the work for me. I call it the Magic Probability Toolkit. Here are the answers it gives.

 

Number of Lands in My Seven-Card Hand	Probability
0	1.3%
1	9.2%
2	24.5%
3	32.3%
4	22.6%
5	8.4%
6	1.5%
7	0.1%

(Do you want to check my math? If you know C++, download the source code for the Magic Probability Toolkit and try it out! It contains the mathematical tools I wrote to help me with my Magic probability calculations. You can see how I did the calculations for this article or use the tools to do entirely new calculations.)

If I graph my results, I can usually get a better feel for the information they contain. So here’s a graph of the probabilities I just calculated.

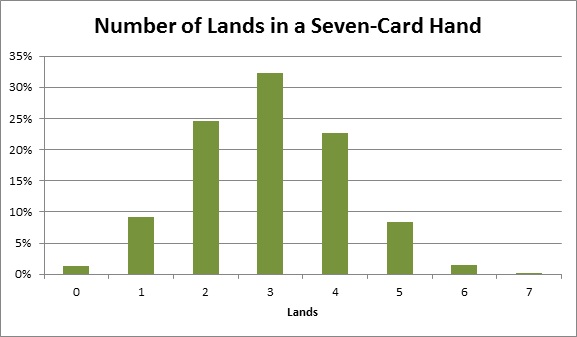
I can see that the most likely draw is a three-land hand. The chance of a three-land hand is 32.3% or about one out of every three hands. That’s nice, since experience tells me that three lands is one of the best hands to get. Two- and four-land hands are both fairly likely as well. The chance of getting zero, six, and seven lands is very, very low. In fact, I should expect to play a thousand games of Magic for every seven-land hand I see!

Mana Screw

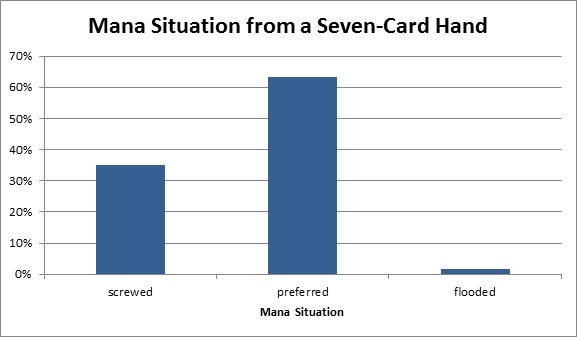
To get a sense of my chances of drawing a good hand versus a bad hand, I’ll group the land counts into categories.

• screwed — 2 or less lands
• preferred — between 3 and 5 lands
• flooded — 6 or more lands

(I’m counting two lands as being mana screwed, but should I? Good question. That’s something I want to look into in more detail in a future article. For now, I’m categorizing it as screwed because I get pretty uncomfortable when I start with two lands. Very different than the warm fuzzies I get from three lands.)

Those categories give these probabilities for how happy I’m going to be with my hand.

 

Mana Situation	Probability
screwed	35.1%
preferred	63.3%
flooded	1.6%

I have a 35% chance of being screwed and a 63% chance of being happy. My chance of being flooded is very low. Here are the numbers in a graph.

Takeaways

Setting aside all of the tables and mathematical explanations, what are the basic takeaways? What useful information have I learned? (I’ll try to end each article with a summary of useful takeaways.)

You’re most likely to draw three land, with two lands coming in second and four lands coming in a close third.

The chance of getting screwed in your opening hand is 35%. That means if you’re the sort of person who mulligans a two-land hand, you will mulligan about one out of every three games. That’s pretty often—basically once a match!

[email protected]
@DanRLN on Twitter