For online play, Wizards offers three different draft queues, offering different payouts, for each block. The 8-4 queue is single elimination, and pays 8 packs to the winner and 4 to the second place finisher. The 4-3-2-2 queue is also single elimination, but pays less to first and second, but pays third and fourth two packs each. Finally, 321Swiss queues offer Swiss drafts and pay out one pack per match win. The Expected Value calculations say the most popular format has the worst EV. What’s going on?
Years ago, Wizards changed the prize payout for drafts. At one time, the drafts paid 5-3-2-2 packs. Later, that was cut to 4-3-2-2, and the 8-4 queues introduced. (Some other changes happened somewhere in there, but I’m not going to dig out my history notes.) Some Magic players have never forgiven Wizards for this change, and continue to attack Wizards, and the payout, in the forums and elsewhere whenever possible. A while back I saw this thread, and initially dismissed it as more of the same. After skimming a bit, I found more than just rants.
The posters were looking at the expected value of the formats, assuming that players had an overall winning average. In other words, if you win, for example, 75% of your matches online, which format maximizes your prize payout.
Obviously, if you lose all your games, your expected value is zero. However, that is true across the board — your expected value is the same in 8-4 as in 321Swiss. If you win every match you play, you will win the most packs in the 8-4 queues. Where it gets interesting is in between. What happens if you win, say, 60% of the matches you play?
The first serious attempt at analysis was done by Ambitious, as described here:
So… wrote some quick Lisp code to check 4-3-2-2 versus 8-4 versus Swiss drafts in terms of average prize per draft. It turns out that there is no whole number of percents where 4-3-2-2 has the best average payout of the three. Up until 49%, Swiss has the best average; at 50%, Swiss and 8-4 are tied; and from 51%. 8-4 leads, I assume all the way up to 100% although I only checked every 1% between 45% and 55%, and every 5% from 25% up to 75%.
[I snipped the code he included.]
My algorithm is basically: If in every b matches you win a times, then if you play b^3 drafts, you’ll win round 1 b^3, divided by b, times a, times. Which is b^2*a (b squared times a). The number of 2nd-round wins of those b^2*a times is b^2*a, divided by b, times a, which is a^2*b (a squared times b). And of those, the number of 3rd round wins is a^3.
So in b^3 drafts, with an a/b chance of winning any match, you’ll win the finals a^3 times, get second (a^2*b) – (a^3) times, and get fourth (b^2*a) – (a^2*b) times. Then multiply those times the prizes for each place, and that’s the function “single-elim” which is the core of the code.
Other posters developed the formulas a bit further. Eventually, bubba0077 graphed the results. Here is his graph, which assumed that the value of the cards obtained in the event, when sold, was about 2 TIX per booster. It also subtracts the cost of the entry fee.
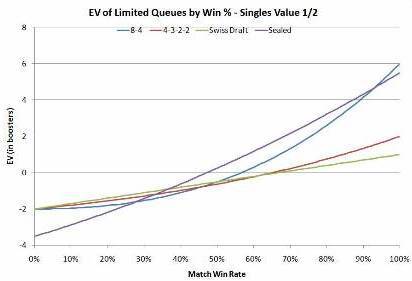
The graph shows a number of interesting things. First of all, it shows that, unless you open expensive cards, or get lucky, drafts don’t pay unless you are reasonably good. That’s not much of a surprise, I guess.
The curve for sealed Swiss events is more interesting. It is a flat payout — two packs per match win — so the line is straight. It is also somewhat higher than the other lines, mainly because a sealed event has you opening 6 packs of product. If the opened product has any value, then the value is going to be 6 times the average value per pack, not three as in drafts. The cost of that product accounts for the high cost for a zero match wins result. In terms of prizes, Wizards is pushing these events, but the public is not really responding all that well. I can think of a number of possible reasons, but I think the fact that drafts are more fun than sealed — at least for most people — is the biggest.
The other thing this graph does clearly show is that, for most people, the 4-3-2-2 queues really do have the worst expected payout. It is the “best” format for people who only win 15% to 30% of their games, in that they are likely to loss less money overall than under other prize structures, but they will still lose.
4-3-2-2 has the worst payout, but is it by far the most popular prize structure. 4-3-2-2 drafts fire more often than any other type. Some of that may be due to people like me, who hate waiting and jump into any queue that has 6 or 7 players already in, but that cannot account for all of it. The first 5 or 6 players in the queue had to have joined for some other reason — not because it was nearly full. And queues for unpopular drafts simply don’t fill. Look at Coldsnap and Mirage block drafts, after all.
Something is wrong in the above analysis. We are either not taking something into account, or some fundamental assumptions are incorrect, or maybe a combination of both. Let’s look at the options.
Economics teaches that people act in a rational manner to maximize their wellbeing — and wellbeing is generally equal to resources, which generally means money. All other things being equal, people should choose the least expensive / most profitable option.
You know, that summarizes over three years of undergraduate and my first year of grad school econ courses. And it isn’t true — which you really don’t learn until sometime after that first year of grad school economics. Now I’m not saying that economics in college is a con job, but…
The simple fact is that human beings are not rational. Evolution has created a number of predilections and preferences that are not strictly rational. Human beings tend to be excellent at pattern recognition, to the point of seeing patterns that are not there. (You know how clothes over a chair at night look like a person, or seeing a friend’s face out of the corner of your eye, only to realize that it is just a stranger in a crowd? Like that.) We have irrational preferences — we buy bottled water for upwards of $10.00 per gallon, listen to [insert your most hated music here], and — well, the list is endless. Stores make their highest profits on impulse buys — the candy and stuff they put near the cash registers, and sell at a huge premium.
I’m not trying to say that the 4-3-2-2 drafts are firing because people are impulse buying. I’m just speculating that other things may be going on as well. Time to list some.
1) People are Risk Averse.
A ton of psychology grad students have earned their PhDs showing that people tend to place more importance on not losing than on winning. For many people, the bet is more attractive than the follow-up double or nothing. Investment advisors understand that avoiding losses is more important, for many people, than earning a high return. That may not be true for true gamblers — and Magic and MTGO have a significant portion of gamblers in the mix — but it is true for a lot of online players. I’m one. For me, it hurts more to come out a draft with nothing that with a smaller prize. I really do like playing the 4-3-2-2s or 321Swiss more, simply because I am far less likely to come away with nothing than in 8-4s. Irrational though it is, I would rather get four packs going 1-1 in two straight 4-3-2-2 drafts than 1-1 and 2-1 in two straight 8-4s. Irrational? Probably — but that does not make it untrue.
To the extent that other people feel the same way, they may also shun the 8-4s. Of course, those people would probably prefer the 321Swiss drafts, since they maximize their chances of winning something. Let’s keep looking.
2) People play for entertainment.
Only some people play only for profit. Others draft because they enjoy the game, the competition, to collect the cards, etc. Years ago, when card prices were much higher and I was much worse, I used to raredraft a lot. I did most of my raredrafting in the 8-4 queues, both because more rares were passed and because I could rationalize not winning more easily. For other drafts, I played mainly in 4-3-2-2s. Once 321Swiss was introduced, I started drafting in that queue more often, because I was more interested in playing a number of games than in winning large prizes.
A number of others have expressed similar goals — they just want to play more games in their drafts. Their chances of getting knocked out in the first round are too high — at least in their judgment — to risk playing in the 8-4s. Their best value, in their judgment at least — is either the 4-3-2-2s or the 321Swiss drafts. For some people, the level of competition in the 321Swiss was too low*, so they draft in the 4-3-2-2 queues.
* The level of competition in the 321Swiss queues is not all that bad. Back when ratings were still visible, I did some analysis, and the 4-3-2-2s and 321Swiss queues were pretty close. Obviously, if you go 0-2 in a 321Swiss queue, the player you will end up facing in round 3 is not going to be great, but otherwise the mix of good and bad is about the same. After the introduction of the monthly championship series, the quality of players in the 321Swiss queue has increased, albeit very slightly.
3) People have time constraints.
Some players have only a limited amount of time to spend on MTGO. They have too many other things going on to devote long periods to online play. This has implications for the events they choose to join.
For these players, 321Swiss drafts may just take too long. The difference is slight — really, the only impact is at the end of the second round, when you may have to wait for three other matches to finish, instead of one. You may also have to wait after the final round for prizes to be distributed, but that only really matters if you need the prize packs to enter another draft. Still, for players that hate waiting, this can be a problem. Those players may favor the 4-3-2-2 queues, as a result.
Finally, I know that I have drafted, on occasion, when I had only an hour or so before I had to leave. In such cases, I could play a round; and maybe two if they were quick. In such cases, I have headed for the 4-3-2-2 queues. I know that I can finish a round or two, and wind up with a couple packs in winnings, or get eliminated from the event early. The 8-4s don’t work at these times, since I am never sure I can play out round 2, and 321Swiss really is too slow.
I don’t think I am unique in this respect, but the number of players that are actually in that circumstance is probably pretty small. The number of players who seek 4-3-2-2 as a compromise between waiting for the round to end and being quickly eliminated is probably reasonably high.
Or the assumptions could be wrong.
The above graph assumed that you could win X% of your matches. That may be a reasonable assumption to make over 5,000 matches of all kinds, but is it reasonable in a draft, either single-elimination or Swiss? Maybe not.
I looked at my match history for FNM over the last year or two. I have won something like 70% of my matches over that time period. We do 8 man pods, Swiss format drafts, and it is pretty unusual for me not to go at least 2-1 (but it does happen.) Overall, about 70%. However, that does not mean that I have a 70% chance of beating any given opponent.
I remember looking around the room before the draft a couple weeks ago. I was wondering who would be in my pod, and I remember sizing up the room. There were a dozen or so players that I was pretty sure I could beat — kids, newer players, and some regular drafters who tended to draft quirky, unstable decks that I could usually simply crush. There were also a couple regular drafters who I knew would give me a battle — people that I beat sometimes, and lost to sometimes. And then there was Sam Black and Brian Kowal. I think I have beaten BK in a sanctioned match once, and it was a back when Extended still had true duals. I can beat Sam maybe once a year, if I am really lucky. I’m sure not 70% – my chance of stealing a match against him are 7%, or maybe 0.7%.
Of course, nothing is a given, which is why we play the games out. I couldn’t count how often someone said to me, at the $5k last weekend, “I just beat deck X. I’m supposed to autolose against that deck,” or “I can’t believe I just lost to deck Y. How can that happen?” That’s why we play the games out — any deck can, with the right mix of luck, skill and opponent misplays, beat any other deck.
Let’s simplify that a bit. Let’s assume that there are three levels of players – 1600, 1700 and 1800. Let’s assume that it is a coin flip when playing a player of the same rating, and that higher ratings always beat lower ratings. (Yes, you can get more elaborate with more levels and an odds of winning factor, but let’s ignore that for now. For now, just three ratings, and auto-wins.)
Let’s further assume that the levels are fairly evenly represented in all draft queues, but the better players tend more towards the 8-4 queue. Since queues have only 8 players, we cannot have three players from each rating. In the 4-3-2-2 queue, the missing rating will be 1800. Lets also assume that, in the 8-4 queue, the missing player will be rated 1600.
The highest rated players will only lose if they are paired against each other, and the odds of that are 1 in 7 (2 in 7 if there are two other 1800 rated players in the draft.) The odds of a lower level player advancing are the same, for the same reason.
Let’s look at a 4-3-2-2:
As an 1700 rated player in a 4-3-2-2, in round 1 I have a certain victory against 3 players, a coin flip against 2 players, and a certain loss against 2 players. My odds of advancing to the second round are therefore 4 in 7, or 57%.
In round 2, the odds are almost 1.7 in 3 that my opponent will be a 1800 player, and I will lose. (Not quite 2 in 3 because the two 1800 may have been paired together and one eliminated.) The odds are 0.3 in 3 that I will face a 1600, and 1 in 3 that I will face another 1700, for a coin flip.
In round 3, under our assumptions, I am almost certain to face a 1800 rated player, and lose in round 3. My expected payout for the 4-3-2-2 draft is, therefore, 2-3 packs.
Now let’s look at an 8-4:
The 8-4, under our assumptions, includes two 1600 players, three 1700 players (including me) and three 1800 players. In round 1, I have a 2 in 7 chance of facing a 1600 player, who I will automatically beat. I have a 2 in 7 chance of the coin-flip / same rating matchup. (Not 3 in 7 — I am one of the 1700s, and I won’t play myself.) I have a 3 in 7 chance of facing an 1800 player and losing. My odds of surviving the round are therefore just 3 in 7.
In round 2, in an 8-4, the odds of a 1600 player being left are 1 in 7. The odds are far higher that the other remaining players in the Top 4 are the three 1800 is much higher. At best, I am going to have a 28% chance of making it to the final round, and winning any prizes.
Assuming that I do make it to the finals, I will be facing an 1800 player, and I will lose. My prize payout will be four packs — and I only get those four packs if I squeak through round 2. With these odds, I can expect to win packs in an 8-4 roughly once every eight drafts, for an EV of 0.5 packs per draft.
You can do the same analysis for the 321Swiss drafts, but that gets a lot more complex. Far more if statements and routines — but the base outcome is that you are far more likely to end up playing against other 1700s, and against 1600s if you are 0-2, or 1800s if you are 2-0. The end result is that you are likely to come out of a Swiss draft, under there assumptions, with about 1.5 packs.
I started to build a spreadsheet that incorporated odds of winning, instead of auto-win or auto-lose. You can build a simple formula of wins and loses, based on difference in rating, and then introduce players with many different ratings into the queues. You can even slant the make-up of the queues. I had a formula that gave each player in a queue a random rating, with a higher expected range for the 8-4s and lower for the 4-3-2-2s and 321Swiss drafts. All I really learned was that the outcome was highly dependent on the initial factors: on the average rating in a queue, of the odds of a given rating beating another, etc. Not quite GIGO, but the assumptions definitely drove the results.
That, in itself, may be the most important finding. The assumptions drive the results — and players’ assumptions about what the queues may hold and their experiences with the queues —drive their choices.
Extrapolating from a sample size of one is always bad, but I understand my motivations better than anyone else’s, so I’ll extrapolate from mine. I choose to play in 4-3-2-2s, or 321Swiss when I would have to wait too long for a 4-3-2-2. I almost never play in an 8-4.
My perception is that the 8-4s are the home of the people that I cannot beat — the Sam Black, Oliver Ruels, and the other people that do the Premium daily drafts columns. My assumption is that, when I face them, I am going to autolose. (Maybe not autolose, but I am risk averse, after all.) My perception, which may be outdated and incorrect but is based on knowledge and experience, is that I will usually be eliminated in an 8-4 before I can win packs. Since I hate finishing an event without any packs far more than I enjoy winning more, I tend to avoid the 8-4s.
On the other hand, I can find a reasonable challenge in the 4-3-2-2s. I can win some packs, and occasionally win the whole draft. I’m not infinite, but I burn through packs reasonably slowly. Maybe I’m a wimp, but it works for me.
I’m generalizing from my own experience, but I think that the same things motivate the other players who frequent the 4-3-2-2 and 321Swiss queues. They don’t feel that they can win 70% of their matches — the figure that they have a reasonable chance to beat 70% of the other players in a draft. So long as they can dodge the ones they can’t beat, or because of their time pressures, expectations or risk aversion, they are happy in the 4-3-2-2s. As for the other players — the ones who value the challenge, or return, above all else? Well, the 8-4 queues rarely lack for players; I expect that’s where they hang out.
PRJ
“one million words” in the 4-3-2-2 queues.

