Limiting Chance is a series that uses mathematics and probability to investigate aspects of Limited play. In this article, I begin a deep dive into the average casting turn of spells, a quantity I previously dubbed "turn cost." Specifically, I look into the impact that mana acceleration has on turn cost.

Turn Cost

Mana cost is a simple concept at face value, but that simplicity belies a deep complexity. It is actually quite hard to fully grasp the repercussions of a spell’s mana cost, to understand the total cost I am paying when I choose to include a card in my deck.

There are two things that make mana cost so hard to grasp.

First of all, mana cost is a nonlinear scale. The difference in impact between a mana cost of five and a mana cost of six is much greater than the difference between the costs one and two. The gap between five and six results in a larger number of turns during which the higher-cost spell sits in my hand uncast. Throughout those turns I am paying an opportunity cost. That spell, if cheaper, would be in play and actively advancing me towards victory.

It is for this reason that I introduced the concept of turn cost. Instead of talking about a card’s cost in terms of how much mana I must pay, I instead talk in terms of how long the card sits in my hand. I define the turn cost of a spell to be the average turn on which I am first able to cast that spell. In games when I draw the spell in my opening hand, that corresponds to the average number of turns the card will be dead. It expresses more accurately than mana cost the true cost of the spell.

The second reason mana cost is a challenge to understand is that its impact varies between decks. In one deck a spell could be fairly easy to cast, while in another deck casting that same spell could be much harder. As an extreme example, consider Geralf’s Messenger at BBB. A bargain in mono-black, but unplayable if black is your splash. A mana cost means different things in different decks. Turn cost, however, takes a deck’s mana base into account. It expresses the cost of the spell in the deck that includes it.

The Basics

I’ve touched on turn cost in a previous article, but only in the context of a standard mana base. I also did not take color into account. In this article, I begin the process of going deeper. First however, let’s review the basics.

In a deck with 40 cards and seventeen lands, looking only at colorless mana costs, here are the turn costs of spells with a range of converted mana costs. I model the effect of mulligans using the rules determined in previous articles.

Even used in this simple way, turn cost is a useful concept. It illustrates the increasing number of turns I must wait for each additional mana in a spell’s mana cost. For low-mana spells, turn cost is nearly equal to mana cost. I only have to wait one turn for each point of mana. For higher-mana spells, turn cost rises much faster than mana cost. For converted mana costs around seven, I am waiting about two turns on average for each point of mana.

Now I will expand on this simple case and look at the impact of my deck’s mana base on turn cost. For simplicity, I will continue to restrict myself to colorless mana costs. In the next article, I will investigate the impact that colored mana has on a spell’s turn cost. I will also look at the turn cost premium paid for spells when they are splashed.

Throughout this article, I use a 40-card deck, and I average between games on the play and games on the draw. All results model the effect of mulligans using the techniques detailed in this article. For decks with a non-standard mana base, a non-standard mulligan goal is sometimes appropriate. In those cases, I state the mulligan goal used. Note that even if you do not agree with the specific mulligan rules determined in previous articles, my technique still gives a good approximation of reasonable mulligan behavior. It does a good job of accounting for the effect that mulligans have on the quantities I calculate. Which exact hands are kept and which are sent back does not significantly alter the results in this article.

Land Count

Let’s look at the effect a deck’s overall land count has on the turn cost of spells in that deck.

My personal default land count in Limited is seventeen. When the deck calls for it, I sometimes bump that number up to eighteen. I know people who play eighteen lands exclusively, and I’ve seen players, especially new players, get greedy and play only sixteen.

Here are the turn costs for colorless spells using various land counts in my deck. For each land count, I use different mulligan rules as appropriate for that land count, with a mulligan goal of four spells and four lands by turn 4.

Looking at the numbers, as well as at the following graph, one thing is clear. Increasing my deck’s land count does not significantly affect the turn cost of low-mana spells. Above four mana, however, the effect is more pronounced. The higher the mana cost of a spell, the larger the impact my deck’s land count has on that spell’s turn cost.

Notice that the first few lands I add above sixteen have the largest impact. As I add lands beyond that, the effect of each land is not as large. I can see this more clearly by focusing in on six-mana spells. Here is a table of how much the turn cost of a six-mana spell drops each time I add an additional land to my deck.

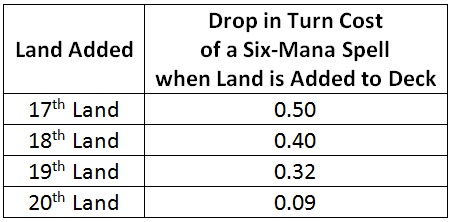
I get the biggest bang for my buck when I add my 17th land. Each land I add after that has an impact, but a diminishing one.

Ramp

What affect does mana acceleration have on turn cost?

Elves

Let’s first look at the effect of Elves. By Elves, I mean any one-drop creature that taps for one mana. Llanowar Elves is the canonical example, while Arbor Elf is the most recent.

In this calculation, I will remove lands from my deck as I add Elves. While I might not actually do that when building a deck, for this calculation I want to keep the number of mana sources in my deck constant. That focuses the calculation solely on the mana acceleration provided by Elves.

I model mulligans using a mulligan goal of four spells and four mana sources, either lands or Elves, by turn 4. I also include the goal of having at least one land on the first turn. (A hand full of Elves with no land is not acceptable.)

Here are the turn costs that result from adding various numbers of Elves to my deck, keeping the number of mana sources in the deck constant at eighteen.

As we already know, Elves allow me to reach higher mana counts more quickly. You can see this most dramatically in the turn cost of three-, four-, and five-mana spells. As I add Elves, the turn cost of those spells drop. Happily, the turn cost of a three-mana spell goes below three with only a single Elf in my deck.

Elves have no impact on the turn cost of one- and two-mana spells. The earliest I could ever cast a two-mana spell is on turn 2. Whether my second mana source is an Elf or a land does not matter.

Notice that the addition of Elves actually increases the turn cost of spells costing nine mana and higher. The effect is very slight. It is because Elves disrupt my mana on the turn they come into play. By the time I can cast spells of such high mana cost, I am generally topdecking mana. If I draw an Elf, I have to wait an entire additional turn before I see any benefit from that Elf. For high-cost spells, Elves are worse than lands.

It is easiest to visualize the effect of Elves on turn cost using the following graph, in which I plot the difference in turn cost between including two Elves in my deck and including with no Elves. You can see that the effect is strongest between three- and five-mana spells. You can also see the turn cost difference crossing above zero at nine mana.

Keyrunes

What about Keyrunes? From a ramp perspective, Keyrunes are much less desirable than Elves since they come out much later. Devoting all of turn 3 to ramp is not nearly as impressive as slipping an Elf out on turn 1, when I probably wasn’t going to do anything meaningful anyway. What impact do Keyrunes have on my deck’s turn costs? (These results of course apply to any three-mana artifact that taps for one mana. Examples abound, such as Chromatic Lantern, Manalith from M13, and the Obelisks of Alara.)

Again I keep the number of mana sources in the deck counting Keyrunes constant at eighteen. I use a mulligan goal of four lands and four spells by turn 4. I do not count Keyrunes as mana sources for the purpose of mulligans.

Here is a graph that illustrates the difference in turn costs between a deck with two Keyrunes and a deck with no Keyrunes.

The turn cost of one-, two-, and three-mana spells is increased. That is due to reducing the number of lands in the deck to make room for the Keyrunes. Notice that the turn cost of a three-mana spell with two Keyrunes is equal to the turn cost of a three-mana spell in a deck with only sixteen lands. (That value is listed in the second table of this article.)

The turn cost of four-mana spells is also increased, but it is not as bad as in a deck with only fifteen lands. If a Keyrune is my fourth mana source, I’m not completely dead in the water. I can use it to cast spells. But depending on the timing of my land draws, the Keyrune can make casting four-mana spells awkward. For example, if I start the game with two lands and a Keyrune and I don’t draw a fourth land until turn 4, I will have to wait until turn 5 before I can cast any four-mana spells. If that Keyrune had been a land instead, with the same draws I could have cast a four-drop on turn 4.

Five-mana spells are the cheapest spells for which Keyrunes provide ramp. That advantage lasts up to casting cost nine. Beyond nine, I am generally in topdeck mode and drawing a Keyrunes slows me down. I cannot cast a high-cost spell on the same turn I draw the Keyrune required to cast it.

Seek the Horizon

Cards like Seek the Horizon are not generally considered ramp, but they do get me to higher mana counts faster. I have used Seek the Horizon once or twice in decks that benefited substantially from a large mana count. A deck that included Grove of the Guardian, Collective Blessing, Vitu-Ghazi Guildmage, and Horncaller’s Chant comes to mind. What effect did Seek the Horizon have on my deck’s turn costs?

Here I keep the deck’s land count constant at seventeen. I use my standard mulligan goal of four lands and four spells by turn 4.

Seek the Horizon has a casting cost of four and thus has no impact until after I can cast a four-mana spell.

Above four mana, Seek the Horizon reduces all turn costs. For a five- or six-mana spell, there is a reasonable chance that I would have been able to cast the spell without Seek the Horizon’s help. So Seek the Horizon provides a small benefit. As casting costs increase, the impact of Seek the Horizon is more pronounced. I’m more likely to need the mana provided to cast the spell.

For a spell like Horncaller’s Chant, I will generally be able to cast the spell more than two turns earlier in a deck that includes two copies of Seek the Horizon. That’s dramatic and goes a long way towards making such spells playable.

Thinning

Cantrips are not ramp by any normal definition of ramp, but they do allow me to dig to my land. When I’m playing a deck with a few low-cost cantrips, I generally feel that my mana base is slightly stronger. Is that a legitimate assessment? What effect do cantrips have on my turn costs?

Here I use a constant land count of seventeen. I use my standard mulligan goal of four lands and four spells by turn 4. I represent cantrips with a one-mana spell that draws a card.

For low-mana spells, cantrips have almost no impact on turn cost. For high-mana spells, the effect becomes significant. Once I am topdecking my land plays, drawing a card puts me one turn closer to the land I need to cast a high-cost spell. So each cantrip I draw puts me one turn ahead.

For high-mana spells, the impact of cantrips corresponds almost exactly to the chance of having drawn one. The longer I have to wait to cast a spell, the more likely I am to draw a cantrip first. Thus the greater the impact cantrips have on turn cost.

Moxen

Just for kicks, here are the numbers for Moxen.

Unlike Elves, Moxen are never worse than land, even for high-man spells. Their effect is diminished, however. When you’re topdecking mana, it doesn’t matter if you draw a land or a Mox.

Takeaways

When you are evaluating a high casting cost card, do not assume that you will be able to cast it on the turn equal to its casting cost. You will likely be casting it somewhat later than that. The higher the casting cost, the more turns you will have to wait for each point of mana.

If you include two mana Elves in a deck, you will cast your three-, four-, and five-cost spells about one-third of a turn earlier averaging across all games played. The effect is smaller for six-cost spells and above.

Including two copies of Seek the Horizon in your deck will allow you to cast an eight-mana spell, such as Horncaller’s Chant, about two turns earlier than normal averaging across all games played. The effect is smaller for lower-cost spells.

Two cantrips in your deck make six-drops castable one-third of a turn early averaging across all games played. The effect is smaller for lower-cost spells.

[email protected]
@DanRLN on Twitter
source code for the Magic Probability Toolkit